Stochastic stabilisation
Contrary to intuition, high frequency noise tends to stabilise motion.
Here we solve the differential equation
x''(t)=(1+Af(t))x(t)
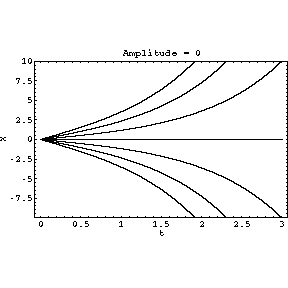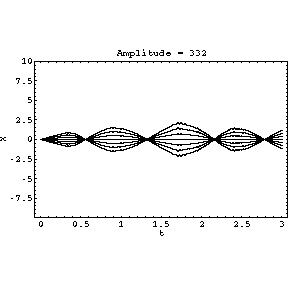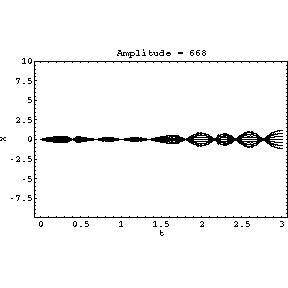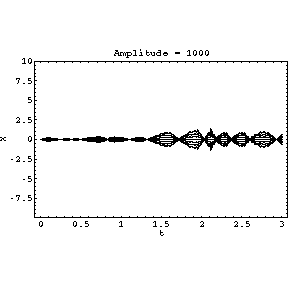
with initial conditions x(0)=0, x'(0)=v with v=-3,-2,-1,0,1,2,3 giving the
separate curves. f(t) is
the noise, given by the sum of 100 terms of the form
cos(
t+
) with
angular frequency given randomly in the interval
(100,500) and phase given randomly in the interval
(0,2
). The amplitude A increases from
0 to 1000 throughout the animation.
When A=0, the solution is simply x=v sinh t, which grows exponentially.
However as A is increased, the solution stabilises to roughly sinusoidal
oscillations.
This equation has many applications, for example it describes small
oscillations of the stochastic Kapitsa pendulum, in which an inverted
pendulum is stabilised by randomly shaking the pivot. The 1 in the
equation denotes the unstable effect of gravity in this instance.
At present, I am mostly considering cosmological applications, in which
photon trajectories in the cosmic microwave background and from distant
galaxies may be stabilised and focussed by gravitational lensing due to the
intervening lumpy matter distribution. See the paper
Stochastic stabilization of
cosmological photons for more details.
Back to home page