Relaxation of a coupled map lattice
Coupled map lattice are dynamical systems with spatially distributed degrees
of freedom, discrete in both space and time, used as simple models of for
example turbulence and ecology. The equations of this "diffusively coupled"
map are
u(x,t+1)=(1-a)f(u(x,t))+a[g(u(x-1,t))+g(u(x+1,t))]/2
f(u)=2u -1
-1
g(u)=-u
where x and t are integers giving the discrete space and time respectively,
u is a real variable, a is a real parameter equal to 0.4 in this simulation,
f(u) is the local dynamics, a well known exactly solvable chaotic map,
and g(u) is the coupling. The initial conditions are randomly distributed
between -1 and 1, and the above dynamics can easily be shown to remain in
that interval.
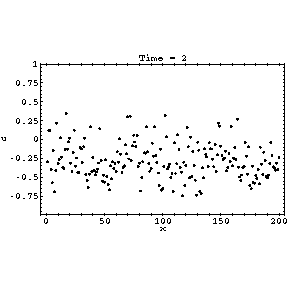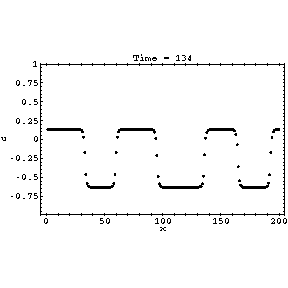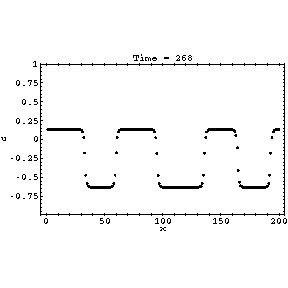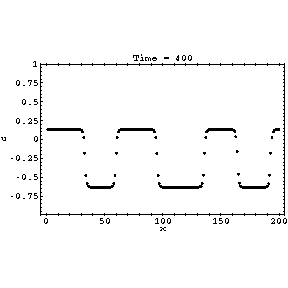
At this parameter value there is a stable period two cycle oscillating between
roughly -0.632 and 0.132. However, distant parts of the lattice might be out
of phase, leading to interesting behaviour at the boundary. Only every
second time step is shown for clarity; for alternate time steps the
picture would be inverted. The relaxation proceeds in three stages:
- The initial random transient very quickly settles into a state with many
domains given by the above two values
- The domains coarsen, with small domains disappearing, until all the
domains remaining are larger than a certain size and stable.
- Boundaries between the domains relax to their permanent states.
At larger values of the parameter, the same behaviour occurs, but over an
exponentially longer time scale. At a=5/9 the 2-cycle merges to form a
stable 1-cycle at a period doubling bifurcation. Further information can
be found in the paper Stable synchronised
states of coupled Tchebyscheff maps.
Back to home page

 -1
-1