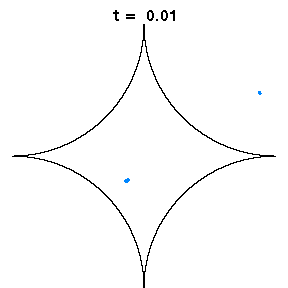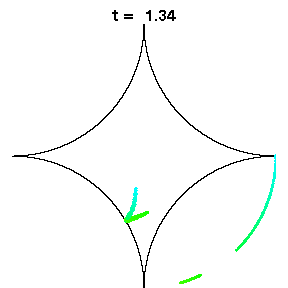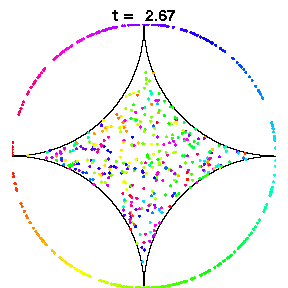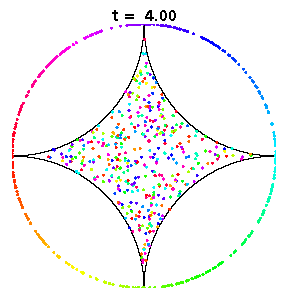
A billiard is a system in which a point particle moves in straight lines except for elastic collisions with the boundary. It is a useful model for all kinds of physical systems involving particles in a homogeneous cavity, or waves if the wavelength is much smaller than the size of the cavity; relevant experimental work has used light, microwaves, sound, electrons and atoms. The dynamics of billiards can vary from completely regular to completely chaotic, depending on the shape of the container.
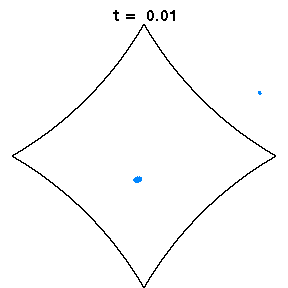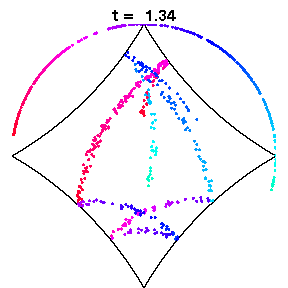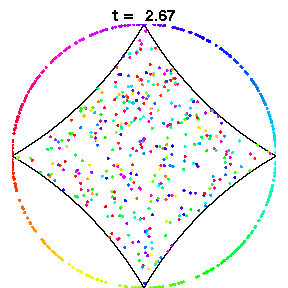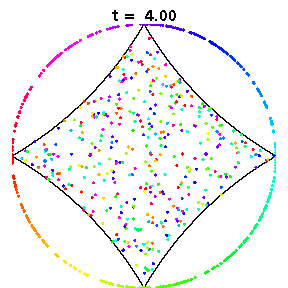
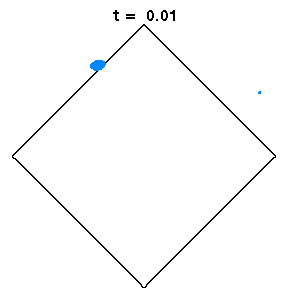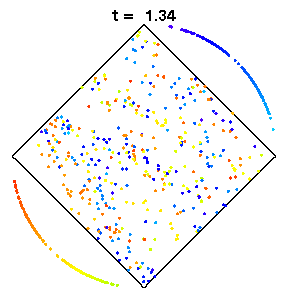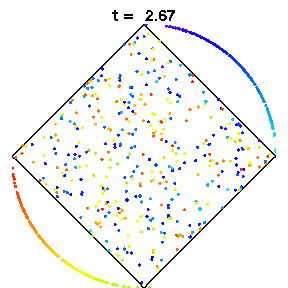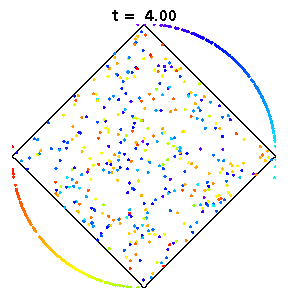
The above animations show diamond billiards, with circular arcs centred at the unit square, and radii 0.5, 1/sqrt(3), 0.7 from left to right. If a system is mixing, that is, initial correlations decay, an initial small bundle of trajectories will fill the phase space uniformly, ie both position and direction (shown here in colour). The time in units of the radius is the same in all three animations.
In the generic case (middle), exponential decay of correlations has been shown for the collision map (discrete time dynamics) and is expected for the flow. Thus mixing occurs in a short time.
The left diamond has cusps (ie zero angle at the vertices), which slows correlation decay in the collision map to 1/n, due to sequences of many collisions near the cusps. However for the flow, the decay of correlations is again very fast, possibly exponential.
The right diamond is almost a square, which is known to be integrable, and hence is not mixing at all. However this model still has slightly curved sides. Here we see that mixing occurs rapidly in position, but very slowly in direction.
Some relevant rigorous results as at March 2017 are as follows: Exponential decay of correlations for finite horizon sinai billiard flows, V. Baladi, M. F. Demers and C. Liverani, arxiv:1506.02836 shows exponential decay of correlations for the flow of dispersing planar billiards without corner points, although it is likely to be extendable to the setting of Spectral analysis of hyperbolic systems with singularities, M. F. Demers and H.-K. Zhang, Nonlinearity 27, 379-433 (2014), which includes the case of corners but not cusps. For cusps, there are results only for the billiard map, with polynomial (not exponential) decay of correlations; see Decay iof correlations for billiards with flat points II: cusps effect H.-K. Zhang, arxiv:1605.07714 and references therein. However, because the time between collisions vanishes at the cusp, much more rapid decay of correlations of the flow is still possible.
See also my publications related to correlation functions.
These animations have been featured in the Bristol Mathematical Ethnographies Project and on Scholarpedia.
Back to home page, publications page.