Drop formation

The ubiquity of drops is beautifully illustrated by this picture of a dolphin, jumping out of the water of the New England aquarium in Boston - the spontaneous formation of drops is a generic feature of flows involving free surfaces. Harald Edgerton's photograph also gives an idea of the challenges involved in the description of free surface flows. The description of the flow shown in the picture would be far beyond the computational capabilities of present day computers. (and it is unlikely that this statement will have to be revised any time soon !) Instead, it is much more fruitful to focus on the individual events of drop separation, which form the essential building-blocks of the flow dynamics. Perhaps it is possible to gain some general insight into the dynamics of drop formation, independent of the particular circumstance under which the drop is formed, or of the type of fluid involved.

Some observations from everyday life indicate that even the formation of an individual drop is more complicated than one might think: to the right is a picture taken at the falls of the Rhine near Schaffhausen, Switzerland. A permanent mist hangs over the falls, apparently composed of droplets small enough to remain suspended in the air. Drop formation thus results in an extremely broad spectrum of different droplet sizes. Remarkably, the origin of this wide distribution of sizes had already been recognised 200 years ago by Felix Savart in Paris. His observations represent quite an achievement, since the separation of a drop of water takes place in the span of perhaps a 1/100 th of a second. Below we show an image of a jet of water being ejected from a nozzle 6 mm in diameter, taken from Savart's paper of 1833. Drops are formed from the jet in a periodic sequence, but in between to main drops, one always finds a much smaller "satellite" drop.

It is the periodicity of the process Savart uses to obtain a time resolution that is far beyond that if his naked eye. Using an especially constructed apparatus, he observed the jet against the background of a moving tape, painted alternately black and white. This amounts to a periodic illumination of the jet, yielding a stationary picture, if its frequency corresponds to the frequency at which drops are formed.

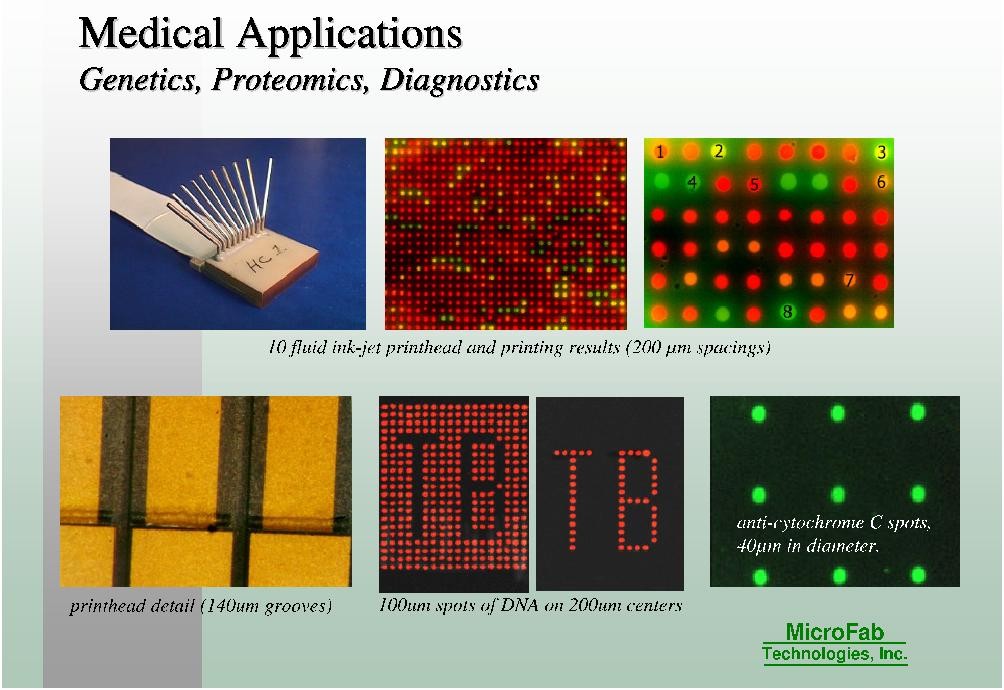
However, it was only in the 1970s, motivated by the advent of ink-jet printing technology, that the consequences of Savart's observations were fully appreciated. This same technology is currently celebrating a revival, owing to its ability of producing a great variety of micron-sized structures. For example, if the ink is replaced by solder, one can print integrated circuits (See the 'solder jet' above). In biotechnology, thousands of DNA-filled water drops can be analysed in parallel, by placing them in an array on a solid surface. All these techniques rely on the production of drops of well-controlled size, and satellite drops are highly detrimental to the quality of the product. A detailed series of images, illustrating the formation of satellite drops, was produced in Bristol as a result of an undergraduate project proposed by Prof. Howell Peregrine (See sequence below). A drop of water was slowly released from a capillary, until gravity overcame surface tension and the drop began to fall. Shortly thereafter, surface tension takes over yet again and pinches the fluid neck, whose radius goes to zero at a point directly neighbouring the drop. Before the neck has a chance to snap back completely into the mass of fluid attached to the capillary, it also pinches on the other end to form a much smaller drop which we have called the satellite.

The satellite drop is thus a residue of the elongated neck formed next to the main drop. The existence of this elongated neck, in turn, is intimately related to the profile close to the point of pinch-off: Toward the drop the profile is quite steep, whereas on the other side it is quite shallow, forcing the neck into a correspondingly elongated shape. The ubiquitous presence of satellites is thus seen to be a consequence of the dynamics close to pinch-off, which always results in a highly asymmetric surface profile. To be able to understand this behaviour, one has to solve the underlying equations of motion close to the point where pinch-off occurs. The fluid motion is characterised by ever smaller length scales (the radius of the shrinking fluid neck), as pinch off is approached. The solution we are looking for should thus be invariant under a change of scale. For the radius h(z,t) of the fluid neck this means that h(z,t) = t' H(z'/t'^{1/2}), where t' = t_0 - t and z' = z - z_0 is the temporal and axial distance from the point where the new drop forms, respectively. This self-similar law means that the shape of profile remains the same as time goes by, the only thing that changes is that the axial and radial length scales of the flow are rescaled in a time-dependent manner. The invariance under a change of scale can also be read off: namely, if the axial position is rescaled according to z' -> alpha z', this change can be absorbed into a rescaling of the time according to t' -> alpha^2 t'.

A confirmation of the self-similar concept is provided by a comparison to experiment. Pictured is a sequence of photographs of a jet, consisting of a glycerol-water mixture, closer and closer to the singular point t'=0. On the right-hand-side one sees the drop, which is moving to the right, and whose centre is marked by a bright spot. The drop is connected to a thin thread, whose radius goes to zero as the singularity is approached. Superimposed on the experimental profiles is the solution of the equations of fluid motion, based on the self-similar structure given above. In particular, the minimum radius of the thread is predicted without adjustable parameters. The predicted profile is extremely asymmetric, consistent with an elongated neck. As we have explined in detail above, it is this peculiar feature of sharp break-up which is responsible for the ubiquitous presence of satallite drops.