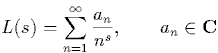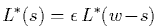ComputeL is a pari package to compute special values of L-functions and their derivatives numerically to high accuracy. It is specifically designed to work with L-functions of motivic origin with an arbitrary number of Gamma-factors, not necessarily distinct. Current version 1.3.8 is implemented as a pari script. As an illustration, it includes examples of computations with

• Riemann zeta-function
• Dirichlet L-functions of Dirichlet characters and Dedekind zeta-function of a number field
• L-functions associated to (H¹ of) curves of genus 1, 2, 3 and 4 over Q, in particular, Birch-Swinnerton-Dyer conjecture for the Buhler-Gross-Zagier elliptic curve of Mordell-Weil rank 3.
• L-functions associated to modular forms and Shintani's zeta-function

    The computations are based on the algorithm from "Computing special values of motivic L-functions". The package applies to L-functions L(s) given by the usual series (for Re s>>0),
        
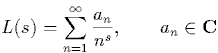
Assume that L(s) multiplied by a suitable product of Gamma-factors,
         
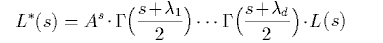
admits a meromorphic continuation to the whole of C. It has, moreover, at most simple poles and is known or conjectured to satisfy a functional equation
        
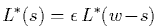
or, slightly more generally, a functional equation relating L*(s) and a "dual" L-function.

To use the package one has to know the parameters of the functional equation (exponential factor A, sign e, weight w, Gamma-factor parameters l₁...l_d) and enough coefficients a_n. Note that there is no restriction on the number d of Gamma-factors and they do not have to be distinct. The poles of L^*(s) have to be known as well, but not necessarily the residues in there. The functions provided allow to perform the following numerical computations with required precision:

• Determine the residues at the poles of  L^*(s) if necessary
• Verify the assumed functional equation numerically
• For a given complex s, compute L(s) or its k-th derivative for a given k

    Download the current version computel.zip (v1.3.8 July 2018). It's a zip archive and can be opened with "unzip -a computel.zip" under most operating systems. Alternatively download separate files below (all are pari scripts).
 

computel	- the package itself
	Basic examples
ex-zeta	- example: Riemann zeta function
ex-chqua	- example: L-function of a quadratic character (Legendre symbol) modulo odd prime p
ex-nf	- example: Dedekind zeta function of a number field
ex-bsw	- example: L-function of an elliptic curve and Birch-Swinnerton-Dyer conjecture
ex-gen2	- example: L-function of a genus 2 curve
ex-shin	- example: Shintani's zeta function
ex-eisen	- example: Eisenstein series of weight k
	Additional examples
ex-chgen	- example: general Dirichlet character (functional equation involves two different L-functions)
ex-delta	- example: L-function of the modular form Delta of weight 12 (unusual coefficient growth)
ex-zeta2	- example: Riemann zeta function for Im(s) large (precision issues)
ex-gen3 ex-gen4	- example: L-functions of a genus 3 and a genus 4 curve    (precision issues when not enough coefficients are given)

For additional examples, see also:

Neil Dummigan's scripts for symmetric powers of L-functions on his publications and preprints page,
Maciej Radziejewski's page Computing zeros of Hecke zeta functions, and
François Brunault's script ex-ellquad computing L(E,1) for an elliptic curve E/Q(sqrt(37)) with everywhere good reduction.

If you have other interesting examples, please drop me an email and I'll include them here. Any other questions, comments and feedback on the package are very much welcome as well. For more advanced features, such as tensor products of L-functions, L-functions of Artin representations, modular forms, elliptic curves over number fields and hyperelliptic curves, see L-functions in Magma.