Quantifying the cost of simultaneous non-parametric
approximation of several samples
Given 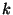 samples
samples
![$(t_{ij},y(t_{ij}))_{j=1}^{n_i}\,\, t_{ij} \in
[0,\,1], i=1,\ldots,\,k$](img2.png) we consider the problem of finding a function
we consider the problem of finding a function
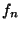 , if any, which is simultaneously an adequate approximation for
all
, if any, which is simultaneously an adequate approximation for
all 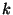 samples. Possible measures of cost are the number of local
extremes, the total variation of
samples. Possible measures of cost are the number of local
extremes, the total variation of 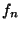 and its derivatives and the
supremum norm of derivatives of
and its derivatives and the
supremum norm of derivatives of 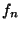 . The costs of a joint
approximation can be comparedwith the costs of approximating each
sample separately. The concept of approximation used is based on
the means of residuals
. The costs of a joint
approximation can be comparedwith the costs of approximating each
sample separately. The concept of approximation used is based on
the means of residuals
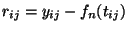 over a family of
subsets
over a family of
subsets 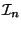 of intervals
of intervals 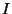 of
of ![$[0,\,1].$](img7.png) .
.