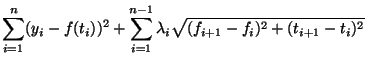Smooth functions and local extreme values
Given a sample of 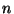 observations
observations
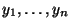 at time points
at time points
 we consider the problem of specifying a function
we consider the problem of specifying a function 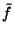 such that
such that 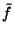
- is smooth,
- fits the data in the sense that the residuals
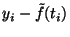 satisfy the multiresolution criterion
satisfy the multiresolution criterion
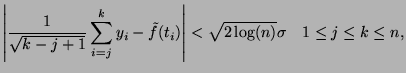 |
(1) |
- is as simple as possible so that
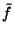 exhibits the minimum number of
local extreme values.
exhibits the minimum number of
local extreme values.
We analyse in particular a fast method
which is based on minimising
where the 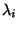 are chosen automatically.
The new method can also be applied to density estimation.
are chosen automatically.
The new method can also be applied to density estimation.