The Lorentz gas is a deterministic model of diffusion, in which a gas of point particles move in straight lines except for mirror-like collisions with circular scatterers. The particles do not interact with each other.
The circular scatterers make the motion highly chaotic, so that correlations decay exponentially with the number of collisions, and if there is maximum time between collisions ("finite horizon" condition), the diffusion is close to that of a random walk, with a Gaussian distribution of displacements of width proportional to sqrt(t) where t is time. The second moment of the distribution converges to the second moment of the Gaussian, and is proportional to the diffusion coefficient.
However, when there is a square array of scatterers as in the animation, there is "infinite horizon", ie particles can move long distances horizontally or vertically without a collision, leading to abnormally rapid diffusion. It has been shown that here also the limiting distribution is Gaussian, but with a faster scaling of sqrt(t log t).
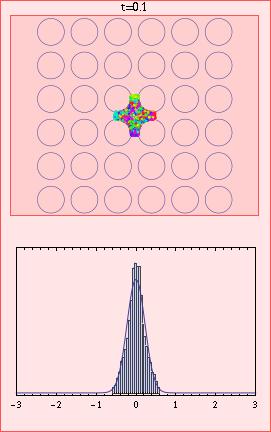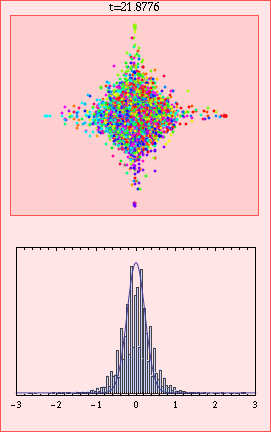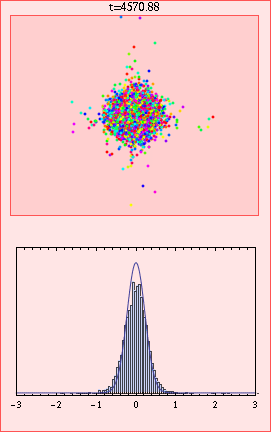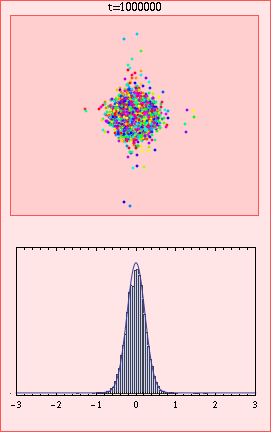
In this animation, the colours in the upper plot correspond to the velocity directions of the 10000 particles, and the lower plot gives a histogram of x values with limiting Gaussian distribution for comparison. For t greater than 2 the axes on both plots are scaled by the factor sqrt(t log t). We can see at around t=10 that there is a cluster of ballistic particles that never collide, and at very large times that convergence to the Gaussian (lower plot) is slow, with a significant excess of particles in the directions of the coordinate axes (upper plot).
Convergence in distribution does not imply convergence of the moments in general. Here, the slow convergence at any fixed scaled displacement, together with the expanding support of the distribution combines to give an interesting anomaly: The second moment of the distribution does not approach that of the limiting Gaussian for long times, in fact it approaches exactly twice this value.
This is discussed, also for higher dimensional Lorentz gases, in "New horizons in multidimensional diffusion: The Lorentz gas and the Riemann Hypothesis," C. P. Dettmann, J. Stat. Phys. 146 181-204 (2012) pdf. See the diffusion page for related papers. More about the infinite horizon Lorentz gas can be found in "Anomalous current in periodic Lorentz gases with infinite horizon", N. Chernov and D. Dolgopyat Russ. Math. Surv. 64 651-699 (2009) and convergence of moments is studied for a slightly different problem in "Convergence of moments for dispersing billiards with cusps", P. Balint, N. Chernov and D. Dolgopyat (preprint, 2012).