Project overview

The current landscape...

The complexity of wireless communication networks has grown considerably in recent years. This has been driven in part by academic research that has started to define the information theoretic boundaries and advantages of certain complex networking topologies and protocols. In parallel, the demands from consumers and industry have pushed wireless networks towards more sophisticated architectures and solutions, primarily in order to ensure a broad range of services can be delivered using a common infrastructure. This is particularly true of 4/5G technologies, which many believe should support all things for all people, including voice, data, public safety, distributed sensing and monitoring, etc.

Analysing complex networks...

A natural consequence of the move toward more complex network structures is that system analysis becomes difficult. However, it is important that engineers do not lose sight of the global structure and properties of complex networks, because such information can be fed into models and optimisation routines so that practical networks can be designed to perform as well as possible.

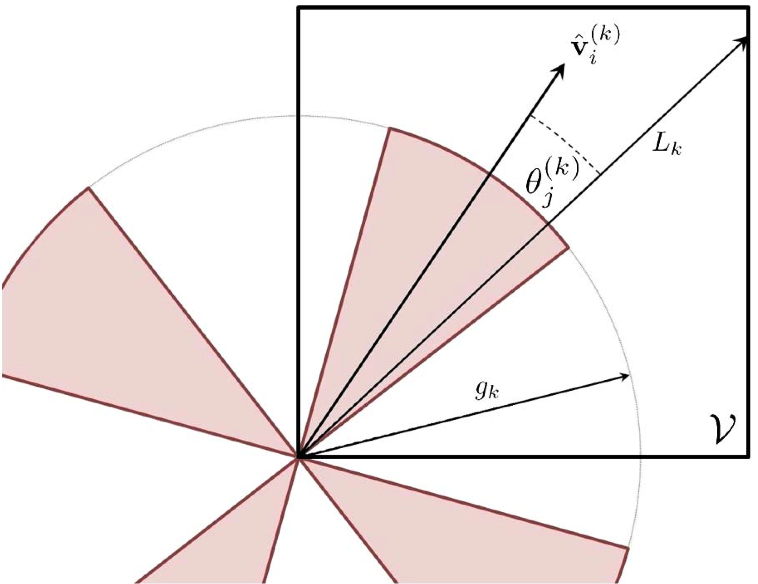
A common approach to tackling complex problems is to exploit the randomness of the underlying system. A typical network deployment may be carefully considered, but taking many such deployments as an ensemble results in a view that suggests device locations and connections are uncertain. Probabilistic approaches to network modelling are not without their difficulties, and some of the main problems that researchers have struggled with over the years arise from the fact that networks are finite entities with physical boundaries. Only a few researchers have treated this issue very recently, and it is the aim of this project to significantly advance this area of research.

New models...

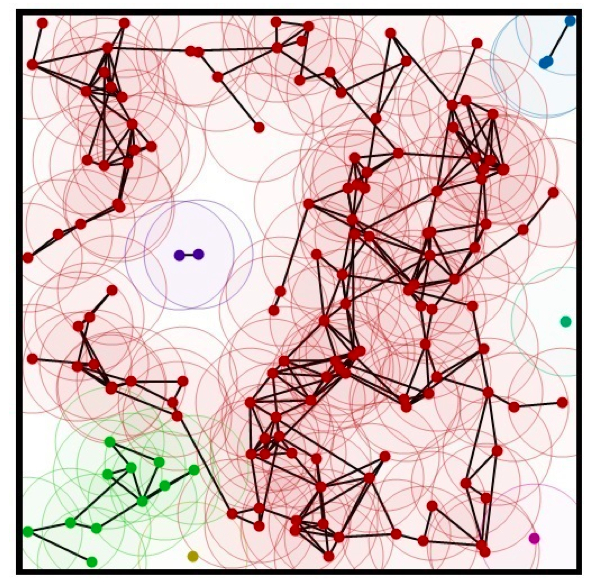
Random geometric graphs (RGG) were introduced by Gilbert in 1961 to study the effects of finite range transmission in models of communication networks. Under this formalism, nodes are randomly distributed on (a subset of) the plane, and all pairs within a fixed range of each other are joined by links (with some probability). RGG models can be related to communication system theory and design, thus making them ideal for studying complex network behaviour.

Recently, focus has shifted to the effects that spatial boundaries have on network connectivity. Notions of resilience and the effects of node directivity, diversity and transmit power have been considered within this context. Even the interplay between higher layer trust protocols and the physical network set-up have recently been explored.

This project...

In this project, the RGG formalism will be exploited further to study several key concepts that influence the structure of spatially embedded networks. The following four topics will be treated:

• continuum models of spatially embedded networks, including the investigation of spectral and centrality properties of soft RGGs
• mobility models in spatially embedded networks, including random waypoint and Levy flight processes
• temporal models of spatially embedded networks, including dynamical node and link (edge) models
• trust models in spatially embedded networks, including trust dynamics and protocol design

The work will take a rigorous mathematical approach, but will always maintain a focus on practical implications and designs, drawing on advice and inspiration from the industrial project partners.

Key research themes

Continuum models

In many practical applications, particularly those related to sensor networks and the Internet of Things, both the density and total number of nodes is made to be relatively large so as to ensure a high degree of connectivity is achieved. For many global network properties, density fluctuations are not relevant on larger scales, suggesting a continuum approach could be adopted for network analysis. Such a separation of scales may facilitate the study of the geometrical effects from the overall shape of the domain, separate from small scale effects due to details of the pairwise connection rules. Conversely, the dependence of network properties on the connection function provides important information on deviations from the continuum limit.

Mobility models

In many mesh network applications, the nodes move, so several "mobility models" have been developed. In order of increasing probability of long paths, these include Brownian motion (BM, a random walk of the node locations), Levy walks (LW, random walk with a power law distribution of long paths) and the random waypoint model (RWP next node location chosen randomly on the whole domain). The temporal properties of these models involve short time correlations for BM and RWP, but long time correlations for LW. Depending on the application, the mobility model may be an empirically determined or a design parameter. Network mobility has been studied extensively; in this project, focus will turn to geometrical aspects.

Temporal models

Network dynamics also result from temporal variations in the node and edge (link) states. In wireless networks, such dynamics arise from variable traffic profiles, CSMA protocols, power conservation and user behaviour. Temporal networks with fixed node positions have received considerable attention across many areas of science, frequently in the context of human, social and disease networks. Generalisations of classical centrality measures (e.g., Katz and accessibility) have also been developed. However, little work on temporal RGGs has been reported, and the influences of boundaries on the dynamics of spatially embedded systems are, as yet, unknown. Such issues will form key focal points in this project.

Trust models

Moving beyond the purely communication-centric notion of connectivity, it is becoming increasingly important to incorporate the notion of trust in wireless network models. Such models inherently consist of two sets of nodes: trustworthy and untrustworthy nodes. This set-up is related to, but fundamentally different than, the so-called AB bipartite graph, wherein nodes in a set A can only connect with each other via nodes in a set B. Other similar models have also been studied in the context of secrecy and network security. Very recently, the existence of a rich theory that quantifies the interplay between trust establishment and the underlying physical network state has been uncovered, which, once developed, will yield insights and design rules that will inform practical network design for sensor applications, cellular device-to-device connections and public safety systems.