Traces and determinants of strongly stochastic operators

C. P. Dettmann

May 15, 1998

Dept. of Physics and Astronomy, Northwestern University, Evanston IL 60208
cpd@snowmass.phys.nwu.edu

Abstract:

Periodic orbit theory allows calculations of long time properties of chaotic systems from traces, dynamical zeta functions and spectral determinants of deterministic evolution operators, which are in turn evaluated in terms of periodic orbits. For the case of stochastic dynamics a direct numerical evaluation of the trace of an evolution operator is possible as a multidimensional integral. Techniques for evaluating such path integrals are discussed. 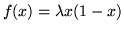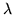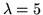Using as an example the logistic map $f(x)=\lambda x(1-x)$ with moderate to strong additive Gaussian noise, rapid convergence is demonstrated for all values of $\lambda$ with strong noise as well as at fixed $\lambda=5$ for all noise levels.

PACS: 05.45.+b 02.50.Ey 02.60.Jh