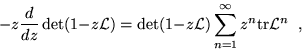Next: Numerical methods
Up: Traces and determinants of
Previous: Introduction
Formalism
The goal is to determine the long time properties of stochastic dynamical
systems, here one dimensional maps with additive noise:
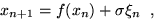 |
(1) |
where f(x) is a known function, for example the logistic map
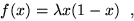 |
(2) |
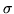 is a measure of the strength of the noise, and
is a measure of the strength of the noise, and
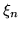 are independent identically distributed random variables with
unit variance,
are independent identically distributed random variables with
unit variance,
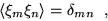 |
(3) |
such as a normalized Gaussian distribution. The methods used
here are equally applicable to 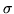 and
and 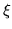 that depend on x, and
non-Gaussian noise distributions.
that depend on x, and
non-Gaussian noise distributions.
Instead of the Langevin form (1) it is more convenient to consider
the discrete Fokker-Planck equation for a probability distribution
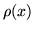 transported by the dynamics and diffusing due to the noise:
transported by the dynamics and diffusing due to the noise:

=\int \delta_\sigma(x-f(x'))\rho_n(x')dx'
\end{displaymath}](img15.gif) |
(4) |
where
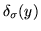 is the noise kernel, for example
is the noise kernel, for example
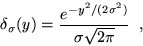 |
(5) |
reducing to a Dirac 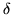 in the deterministic
in the deterministic 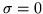 limit.
limit.
Long time properties of the dynamics are obtained from the leading
eigenvalue(s) of the linear evolution operator 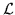 ,
which are
(the inverses of) solutions of the characteristic equation
,
which are
(the inverses of) solutions of the characteristic equation
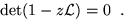 |
(6) |
For example, the probability of a point initially in an open system
remaining there after n iterations is typically proportional to
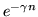 where the escape rate
where the escape rate 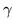 is related to the
leading zero z0 by
is related to the
leading zero z0 by
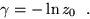 |
(7) |
Dynamical averages and diffusion coefficients can be obtained from the
leading zero of appropriately weighted evolution operators [1,2,3].
The spectral determinant (6) of an infinite dimensional operator
may be defined by its cumulant expansion in powers of z, using the
matrix relation
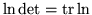 and Taylor expanding the logarithm:
and Taylor expanding the logarithm:
Cn may be obtained from all the traces
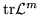 with
with 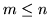 ,
and an approximation for z0 is obtained by numerical
root finding on the n'th degree polynomial given by the truncation of
the determinant. The above expression for Cn quickly gets complicated;
it is easier to expand the derivative
,
and an approximation for z0 is obtained by numerical
root finding on the n'th degree polynomial given by the truncation of
the determinant. The above expression for Cn quickly gets complicated;
it is easier to expand the derivative
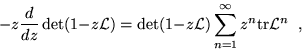 |
(9) |
which leads to the recursive equation
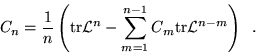 |
(10) |
The trace is straightforward to write down as an n-dimensional integral,
a discrete periodic chain reminiscent of a path integral, obtained in
Ref. [13],
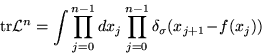 |
(11) |
where the index j is cyclic, so xn=x0. In the noiseless (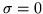 )
limit, the integrand is a product of Dirac
)
limit, the integrand is a product of Dirac 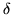 -functions, and the
trace is given by a sum over the fixed points of fn, that is, the
n-cycles of f. In Refs. [10,11] the weak noise limit is
obtained by a saddlepoint expansion of the integral around these cycles.
Here, the integral is performed numerically, up to n=5, as described in the
following section.
-functions, and the
trace is given by a sum over the fixed points of fn, that is, the
n-cycles of f. In Refs. [10,11] the weak noise limit is
obtained by a saddlepoint expansion of the integral around these cycles.
Here, the integral is performed numerically, up to n=5, as described in the
following section.



Next: Numerical methods
Up: Traces and determinants of
Previous: Introduction
Carl Philip Dettmann
1998-05-15
![]() transported by the dynamics and diffusing due to the noise:
transported by the dynamics and diffusing due to the noise:
![]() ,
which are
(the inverses of) solutions of the characteristic equation
,
which are
(the inverses of) solutions of the characteristic equation
![]() and Taylor expanding the logarithm:
and Taylor expanding the logarithm: