WaveThresh
Help
CWavDE
Wavelet Density estimation
DESCRIPTION
One-dimensional wavelet density estimation
(does not automatically estimate parameters).
The code written by David Herrick is more sophisticated.
USAGE
CWavDE(x, Jmax, threshold = 0, nout = 100, primary.resolution = 1,
filter.number = 10, family = "DaubLeAsymm", verbose = 0,
SF = NULL, WV = NULL)
REQUIRED ARGUMENTS
- x
- A vector (of any length) containing data whose density you wish to
estimate.
- Jmax
- The number of levels to use in the wavelet transform (user must select).
OPTIONAL ARGUMENTS
- threshold
- If set then the derived wavelet coefficient will be subject to hard
thresholding with the threshold value supplied (nb this value is
NOT chosen automatically and needs to be chosen by the user for proper
use).
- nout
- The number of ordinates for the resultant density estimate
(needs to be chosen by the user for best performance).
- primary.resolution
- The primary resolution for the scaling functions that the data, x, gets
projected onto
(needs to be chosen by the user for best performance).
- filter.number
- Specifies the family member of the wavelet family (see
filter.select for more details). Only used
if the
SF argument is not specified.
(Needs to be chosen by the user for best performance).
- family
- specifies the family of wavelets that you want to use (see
filter.select for more details).
(Needs to be chosen by the user for best performance).
- verbose
- Controls the printing of "informative" messages. There aren't many.
- SF
- A list with two components x and y. These are the (x,y) values of the
scaling function to use (if this argument is not specified then the
function uses the support function to generate
appropriate values using
filter.number and family
arguments above).
- WV
- A list with two components x and y. These are the (x,y) values of the
mother wavelet to use (if this argument is not specified then the
function uses the support function to generate
appropriate values using
filter.number and family
arguments above).
VALUE
A list with the following
components
- x
- X coordinate of density estimate (of length nout)
- y
- y coordinate of density estimate (of length nout).
- sfix
- The range of k translation values for the scaling functions used
at the finest level.
- wvixmin
- The minimum of the k translation values for the wavelets at each of
the Jmax scale levels.
- wvixmax
- The maximum of the k translation values for the wavelets at each of
the Jmax scale levels.
SIDE EFFECTS
None.
DETAILS
Computes a one-dimensional wavelet based density estimate. You might
also like to look at the code written by David Herrick.
This code follows the procedure for computing wavelet density estimates
espoused by Hall and Patil, 1995.
First, scaling function coefficients at a given primary resolution are
computed by projection of the X_i values onto the father wavelets, \phi_i
for all coefficients of father wavelets whose support covers X_i.
The resulting father wavelet coefficients are then subjected to a Jmax
level wavelet transform. Thresholding is applied and then the estimate
is constructed from the thresholded wavelet coefficients.
This piece of code is not really designed to do production density estimation
but to be an exploratory tool for evaluating procedures that automatically
compute parameter estimates (threshold, primary res, Jmax, etc).
RELEASE
Version 3.6 Copyright Guy Nason 1995
SEE ALSO
support.
EXAMPLES
#
# Generate some example data. A bimodal hump!
#
x <- c( rnorm(100, -2, 1), rnorm(100, 2, 1))
#
# Subject this to a wavelet density estimate.
#
tmp <- CWavDE(x, Jmax=10)
#
# Note this is not a "serious" estimate since the values of primary.resolution,
# threshold, filter.number and family would have to be chosen properly (and
# Jmax).
#
#
# Plot the estimate
#
plot( tmp$x, tmp$y, type="l")
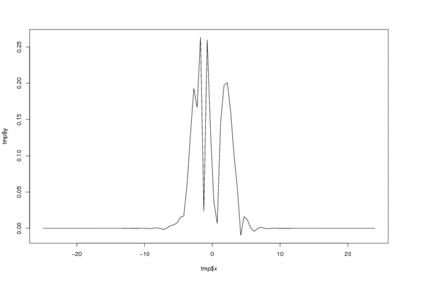 #
# Well, sort of bivariate! Let's make it a bit smoother.
#
# The following parameters were chosen by trial and error
#
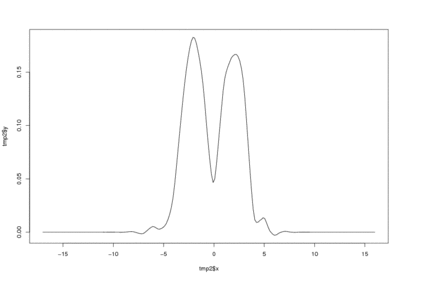
tmp2 <-CWavDE(x, 10, filter.number=6, nout=200, primary=1, threshold=0.07)
#
# Plot the new estimate
#
plot( tmp2$x, tmp2$y, type="l")
#
# Well, sort of bivariate! Let's make it a bit smoother.
#
# The following parameters were chosen by trial and error
#
tmp2 <-CWavDE(x, 10, filter.number=6, nout=200, primary=1, threshold=0.07)
#
# Plot the new estimate
#
plot( tmp2$x, tmp2$y, type="l")
 #
# Well, sort of bivariate! Let's make it a bit smoother.
#
# The following parameters were chosen by trial and error
#
tmp2 <-CWavDE(x, 10, filter.number=6, nout=200, primary=1, threshold=0.07)
#
# Plot the new estimate
#
plot( tmp2$x, tmp2$y, type="l")
#
# Well, sort of bivariate! Let's make it a bit smoother.
#
# The following parameters were chosen by trial and error
#
tmp2 <-CWavDE(x, 10, filter.number=6, nout=200, primary=1, threshold=0.07)
#
# Plot the new estimate
#
plot( tmp2$x, tmp2$y, type="l")
