[home]

[research]

[publications]

[cv]

[links]

[quantum chaos]

[dynamical systems]

[number theory]

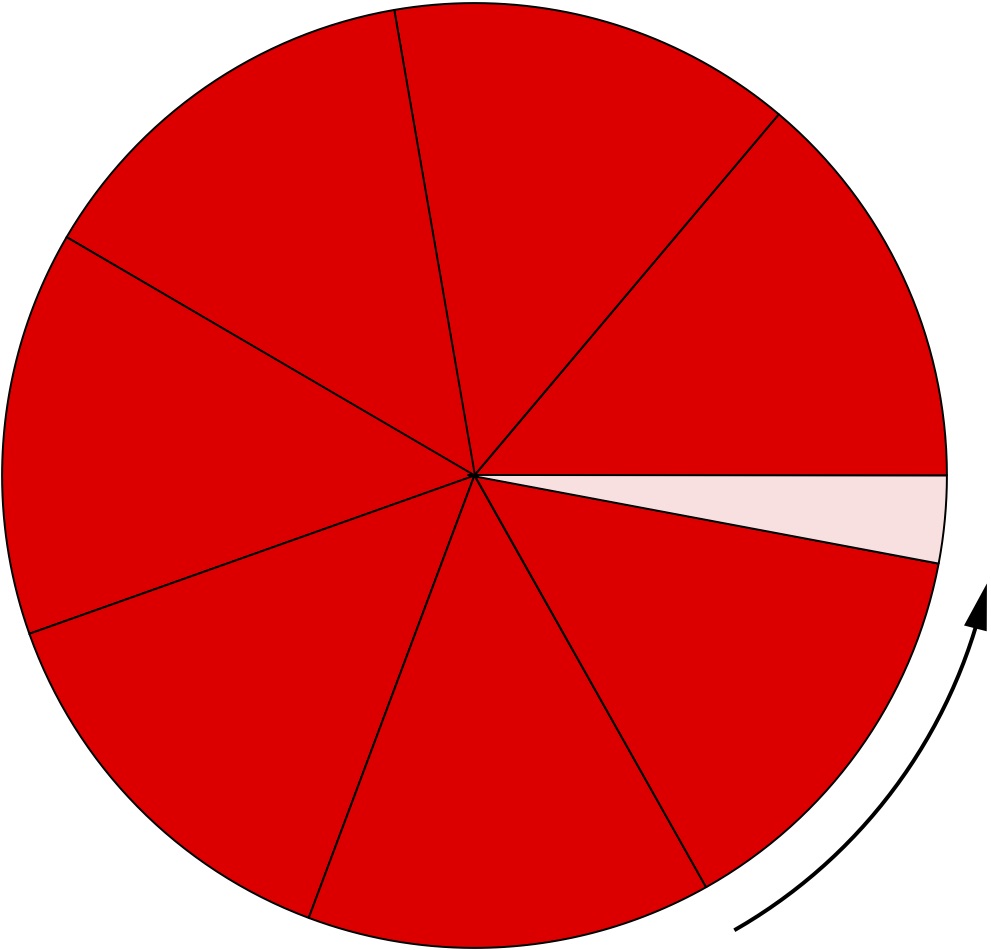
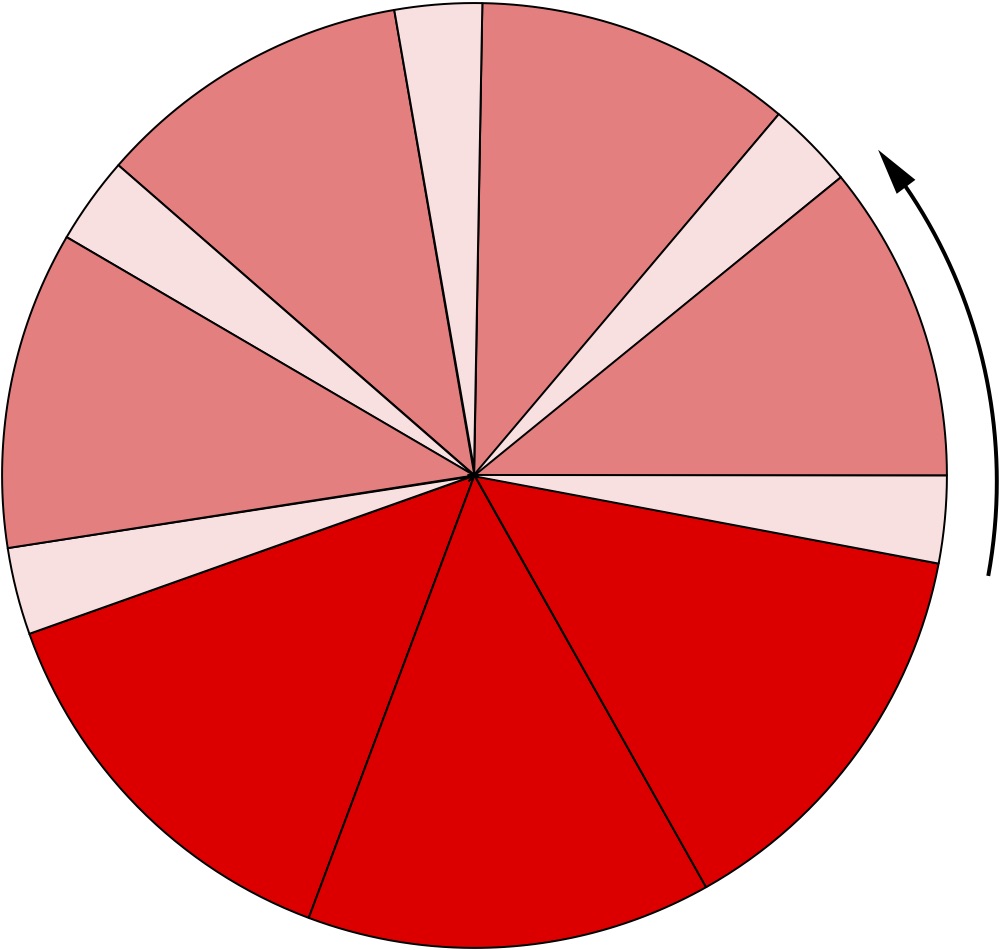
Imagine we divide a cake by cutting a first wedge at a given angle, then an identical second, third, and so on as illustrated below, until the remaining piece is either of the same size as the previous, or smaller. We now have a cake comprising wedges of at most two distinct sizes: the size of the original and that of the left-over wedge. Suppose we continue cutting but insist that after each cut we rotate the knife by the same angle as before. How many different sizes of cake wedges are there after N cuts?



The celebrated "three gap theorem" states that for each N there will be at most three! This surprising fact was understood by number theorists in the late 1950s. Various new proofs have appeared since then, with connections to continued fractions, Riemannian geometry and elementary topology, as well as higher-dimensional generalisations. A simple proof of the three gap phenomenon, which exploits the geometry of the space of two-dimensional Euclidean lattices, can be found in J. Marklof and A. Strömbergsson, The three gap theorem and the space of lattices, American Mathematical Monthly 124 (2017) 741-745.