Jens Marklof's publications
Quantum mechanics tells us that microscopic particles,
such as electrons or atoms, are not solid masses but rather behave
like interfering waves. The theory of quantum chaos explores the
wave dynamics in chaotic geometries, and compares it with the
corresponding classical motion of macroscopic particles.
Here we present recent research on a mathematical
model of quantum chaos, a quantum map, which captures
many essential features of realistic chaotic quantum systems.
Before the invention of quantum mechanics it was believed that
the physical laws governing atoms and electrons are
of the same type as those for the planets in the solar system. This theory
of classical mechanics was however unable to explain that
atomic energy levels are in fact discrete, quantised.
The revolutionary idea of quantum mechanics is that particles
can interfere with each other in the same way as light or radio waves do.
The discreteness of atomic energies then follows from a similar
mathematical argument as that for resonances in wave theory.
Chaos is a concept of classical mechanics. We say a system
is chaotic if the trajectory of a particle (e.g., an asteroid
in the solar system) is exponentially sensitive to the choice of
its initial position.
In quantum mechanics, due to Heisenberg's uncertainty principle, the
notion of a particle trajectory does no longer make sense, nor does
the traditional notion of chaos. So what is quantum chaos?
The main task in the theory of quantum chaos is to find universal statistical
signatures in the quantum energy levels and the distribution of
wave intensities of the particle, which correlate with the degree
of chaos in the underlying classical dynamics.
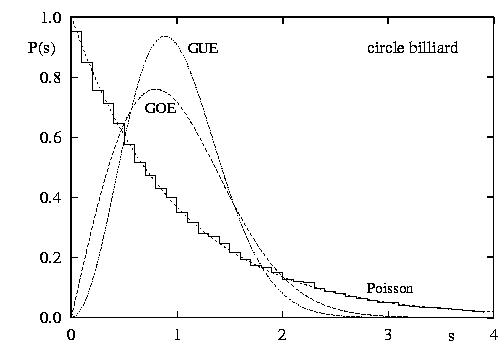
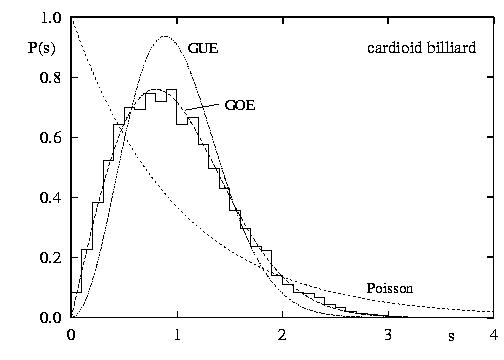
The figure above shows the distribution of gaps between the energy levels
of an electron confined to a circular domain (left) and a heart-shaped
domain (right).
The classical dynamics in the circular domain is integrable (i.e.,
non-chaotic),
and the gaps between quantum energy levels follow an exponential distribution
characteristic for uncorrelated random
numbers. On the other hand, the classical dynamics in the cardioid is
chaotic, and the statistics are well modelled by the gap distribution of
eigenvalues of large matrices chosen at random
from the Gaussian Orthogonal Random Matrix Ensemble (GOE).
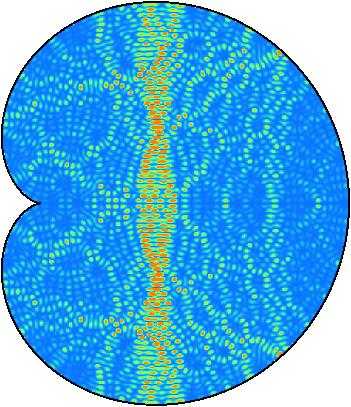
Below is the image of the intensity distribution of
two quantum wave functions (eigenstates)
of an electron confined to the cardioid. (Blue corresponds to low, Yellow to
medium and Red to high intensity. Courtesy of
A. Bäcker, TU Dresden)
One of the central theorems in quantum chaos (Shnirelman's quantum
ergodicity theorem) says that, if the underlying classical dynamics is
chaotic, then almost all eigenstates look as the one
above on the left, in that they are uniformly distributed over the
whole domain. Localised eigenstates such as the one above right are very rare
and it is not clear whether these still exists at very high energies,
i.e., small wave lengths.
The mathematical analysis of systems of the above type is rather involved.
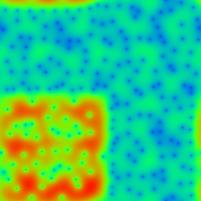
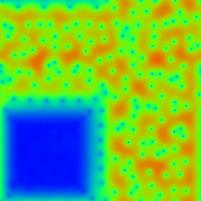
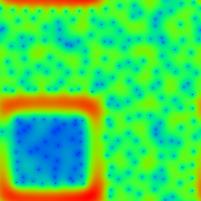
Below is a display of two eigenstates of a quantum map which
is more accessible to rigorous techniques. The corresponding classical
dynamics is here in fact mixed.
The dynamics in the L-shaped region highlighted in the right image is chaotic,
while the dynamics in the complement, the small square highlighted on the
left, is trivial (i.e., every point is classically mapped to itself).
The central result of our research, published in the journal
Nonlinearity, is that
25% of all quantum eigenstates localise completely on the small square
(the eigenstate on the left is one example), and 75% of all eigenstates
are uniformly distributed on the L-shaped region
(the eigenstate displayed on the right is one example for this behaviour).
We have also observed some rare eigenstates which localise on the boundary
between the chaotic and integrable domain; two examples of such
eigenstates are displayed below.
The question of the existence of such eigenstates at arbitrarily small wave
length remains an interesting challenge for future research.
A better understanding of quantum localisation may well have important
applications to conductance properties of micro-electronic devices.
For more information see
J. Marklof and S. O'Keefe,
Weyl's law and quantum ergodicity for maps with divided phase space,
with an appendix by S. Zelditch, Nonlinearity
18 (2005) 277-304.