WaveThresh
Help
makegrid
Interpolate data to a grid.
DESCRIPTION
This function takes a set of univariate (x,y) data with x arbitrary
in (0,1) and linearly interpolates (x,y) to an equally spaced dyadic grid.
USAGE
makegrid(t, y, gridn = 2^(floor(log(length(t)-1,2)) + 1))
REQUIRED ARGUMENTS
-
t
- A vector of
x data.
Each of the entries of x must lie between 0 and 1.
-
y
- A vector of
y data. Each entry of y corresponds
to the same-positioned entry in x and so y
must be of the same length as x.
OPTIONAL ARGUMENTS
-
gridn
- The number of grid points in the dyadic grid that the (x,y) gets
interpolated to. By default this is the next power of two larger
than the length of
x.
VALUE
An object of class griddata.
SIDE EFFECTS
None
DETAILS
One method for performing wavelet regression on data that is not
equally spaced nor of power of two length is that described in
Kovac, (1997) and
Kovac and Silverman, (2000).
The Kovac-Silverman algorithm linearly interpolates arbitrarily spaced
(x,y) data to a dyadic grid and applies wavelet shrinkage to the
interpolated data. However, if one assumes that the original data obeys
a signal+noise model with iid data the interpolated data will be
correlated due to the interpolation. This fact needs to be taken into
account after taking the DWT and before thresholding one realizes that
each coefficient has its own variance. The Kovac-Silverman algorithm
computes this variance efficiently using knowledge of the interpolation
scheme.
RELEASE
Version 3.9.6 Copyright Arne Kovac 1997
Copyright Guy Nason (help pages) 1999
SEE ALSO
accessc,
doppler,
griddata object,
irregwd,
newsure,
plot.irregwd,
threshold.irregwd,
EXAMPLES
#
# Generate some values in (0,1), then sort them (for plotting)
#
tt <- sort(runif(100))
#
# Now evaluate the doppler function and add
# some noise.
#
yy <- doppler(tt) + rnorm(100, 0, 0.15)
#
# Now make the grid with this data
#
yygrid <- makegrid(t=tt, y=yy)
#
# Jolly good. Now let's take the wavelet transform of this gridded data.
# Note that we have to use the irregwd function
# of the gridded data as it computes the variances of the coefficients
# as well as the coefficients themselves.
#
yyirregwd <- irregwd(yygrid)
#
# You might want to plot the coefficients
#
# If you want to see the actual coefficients you have to first convert
# the class of the yyirregwd object to a wd object and then use
# plot.wd like this
#
yyirregwd2 <- yyirregwd
class(yyirregwd2) <- "wd"
plot(yyirregwd2)
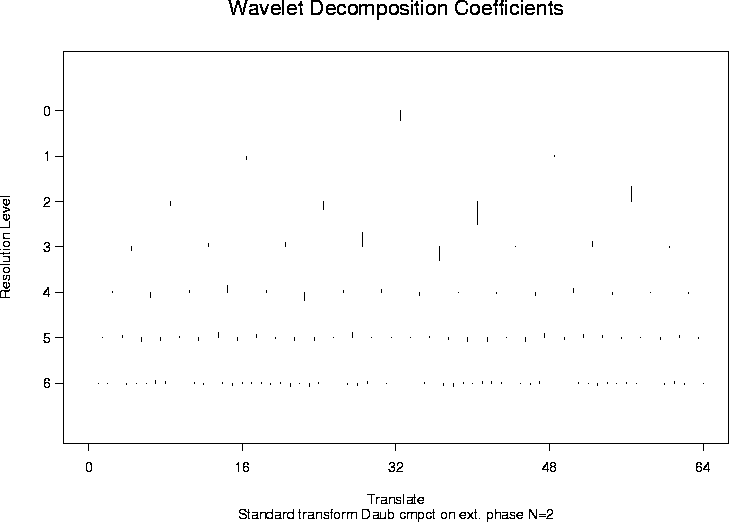 #
# If you want to see the variance factors (essentially the coefficient
# variances divided by the overall variance). Then just use
# plot.irregwd
#
plot(yyirregwd)
#
# If you want to see the variance factors (essentially the coefficient
# variances divided by the overall variance). Then just use
# plot.irregwd
#
plot(yyirregwd)
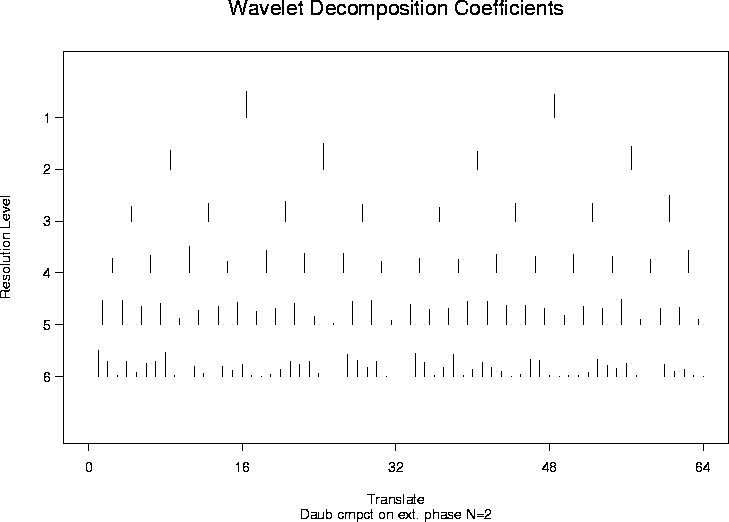 #
# Ok. So you've seen the coefficients. Now let's do some thresholding.
#
yy.thresh.sure <- threshold(yyirregwd, policy="sure", type="soft", dev=madmad)
#
# And now do the reconstruct
#
yy.wr <- wr(yy.thresh.sure)
#
# And you can even plot the answer on the new grid!
#
plot(yygrid$gridt, yy.wr, type="l")
#
# And superimpose the original data!
#
points(tt, yy)
#
# Ok. So you've seen the coefficients. Now let's do some thresholding.
#
yy.thresh.sure <- threshold(yyirregwd, policy="sure", type="soft", dev=madmad)
#
# And now do the reconstruct
#
yy.wr <- wr(yy.thresh.sure)
#
# And you can even plot the answer on the new grid!
#
plot(yygrid$gridt, yy.wr, type="l")
#
# And superimpose the original data!
#
points(tt, yy)
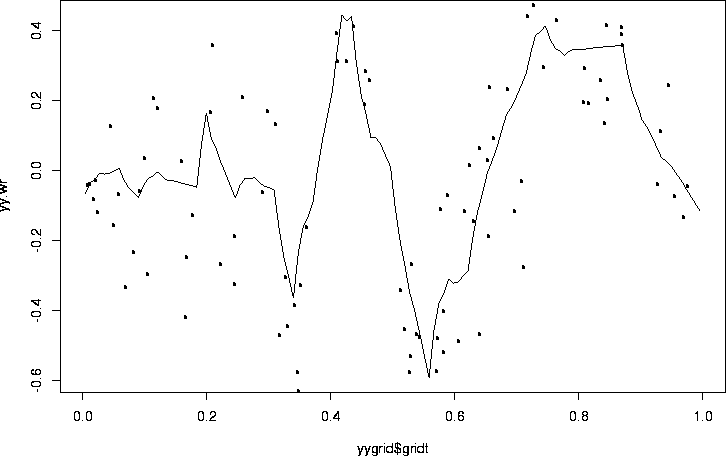 #
# This is sort of Doppler like!
#
# This is sort of Doppler like!
 #
# If you want to see the variance factors (essentially the coefficient
# variances divided by the overall variance). Then just use
# plot.irregwd
#
plot(yyirregwd)
#
# If you want to see the variance factors (essentially the coefficient
# variances divided by the overall variance). Then just use
# plot.irregwd
#
plot(yyirregwd)
 #
# Ok. So you've seen the coefficients. Now let's do some thresholding.
#
yy.thresh.sure <- threshold(yyirregwd, policy="sure", type="soft", dev=madmad)
#
# And now do the reconstruct
#
yy.wr <- wr(yy.thresh.sure)
#
# And you can even plot the answer on the new grid!
#
plot(yygrid$gridt, yy.wr, type="l")
#
# And superimpose the original data!
#
points(tt, yy)
#
# Ok. So you've seen the coefficients. Now let's do some thresholding.
#
yy.thresh.sure <- threshold(yyirregwd, policy="sure", type="soft", dev=madmad)
#
# And now do the reconstruct
#
yy.wr <- wr(yy.thresh.sure)
#
# And you can even plot the answer on the new grid!
#
plot(yygrid$gridt, yy.wr, type="l")
#
# And superimpose the original data!
#
points(tt, yy)
 #
# This is sort of Doppler like!
#
# This is sort of Doppler like!