These pages sorted by the size of $t$
These pages sorted by the size of $Z(t)$
These pages sorted by the size of $S(t)$
Here are some pictures of and information about $Z(t)$ and $S(t)$ for some large values of $t$. The $Z$ function is the zeta function on the critical line, rotated so that it is real, so \[ Z(t) = e^{i Arg(\zeta(1/2 + it)} \zeta(1/2 + it) \] $S(t)$ is the argument of $\zeta(1/2 + it)$, properly interpreted. In some way, it measures irregularity in the distribution of the zeros of the zeta function.
These are from computations run by Ghaith Hiary and myself, based on the algorithm described in Ghaith's paper (also available at the arXiv). These computations have been run on a variety of machines. Initially, we used machines on the Sage cluster at the University of Washington (thanks to William Stein and the NSF), then later the riemann cluster at University of Waterloo (thanks to Mike Rubinstein). Currently, computations are being run at the University of Bristol on the LMFDB machines (funded by EPSRC) and on BlueCrystal.
If your web browser window is big enough, in the top right of each section below you will see a plot of Z(t), in the bottom left you will see S(t), and in the bottom right you will see a zoomed in plot of Z(t). Things are sized roughly so that this looks good on my 1080p monitor.
The images are all links that will take you to a zoomable version of the plot.
You can click on any image for a bigger version. Also, you can look at a list of all of the images: Z(t) or S(t).
See also:
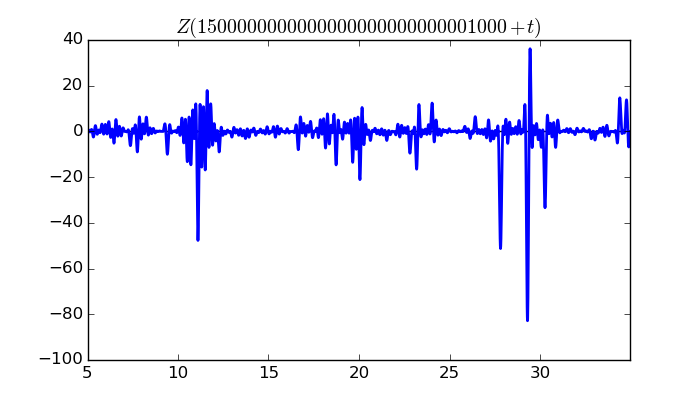
$\zeta(1/2 + it)$ around $t = 1500000000000000000000000001000 \approx 1.5 \times 10^{ 30 }$
Largest value of $Z(t)$ in this graph:-82.82322625
Value of $t$ for which the maximum occurs:1500000000000000000000000001029.30549609
Value of $\zeta(1/2 + it)$:$70.97317311 + 42.69069576i$
Maximum of $S(t)$ in this range:1.922620206
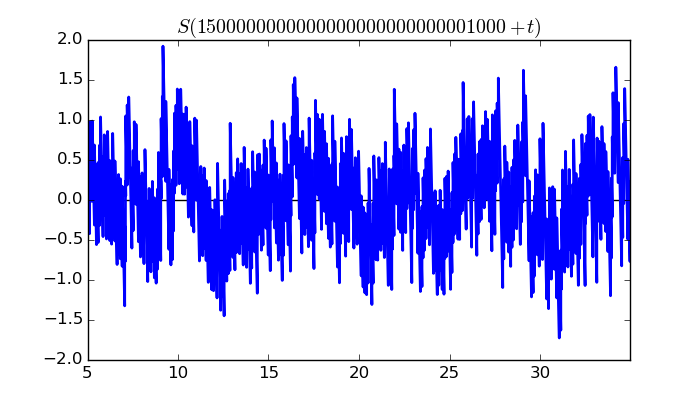
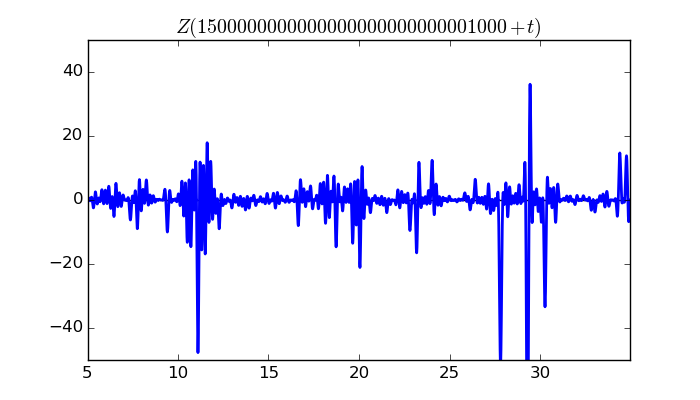
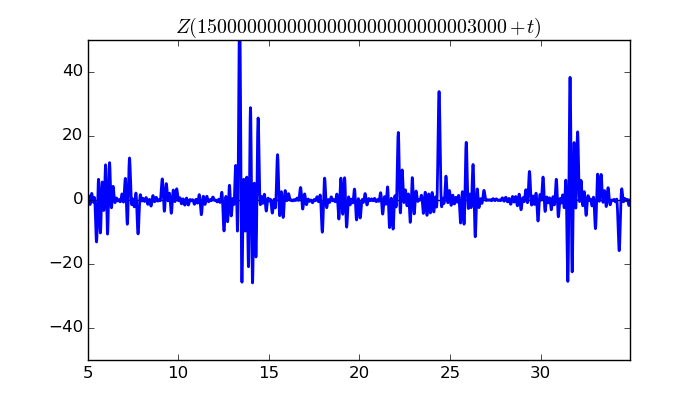
$\zeta(1/2 + it)$ around $t = 1500000000000000000000000003000 \approx 1.5 \times 10^{ 30 }$
Largest value of $Z(t)$ in this graph:58.92508758
Value of $t$ for which the maximum occurs:1500000000000000000000000003013.39599609
Value of $\zeta(1/2 + it)$:$28.72706915 + 51.44824044i$
Maximum of $S(t)$ in this range:1.920177045
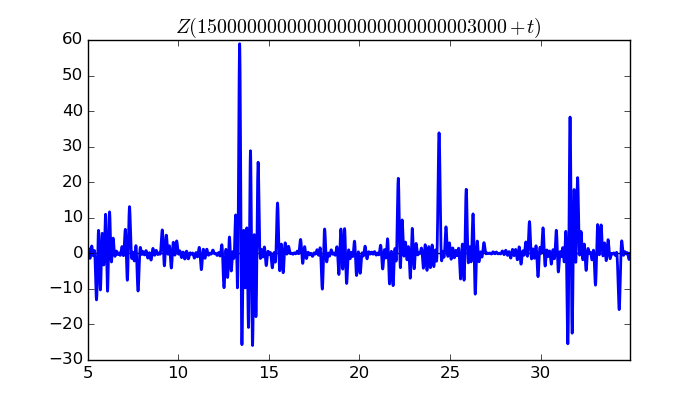
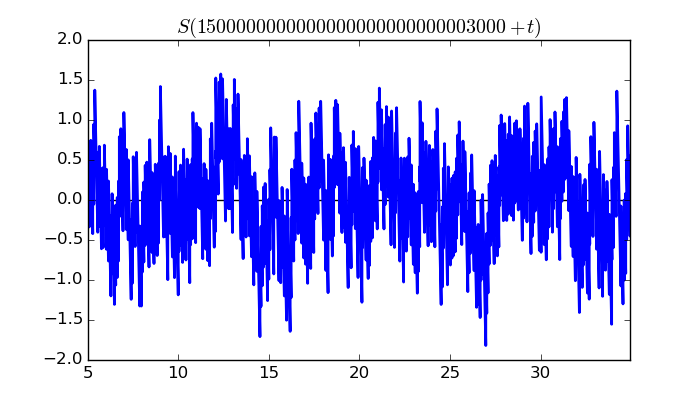
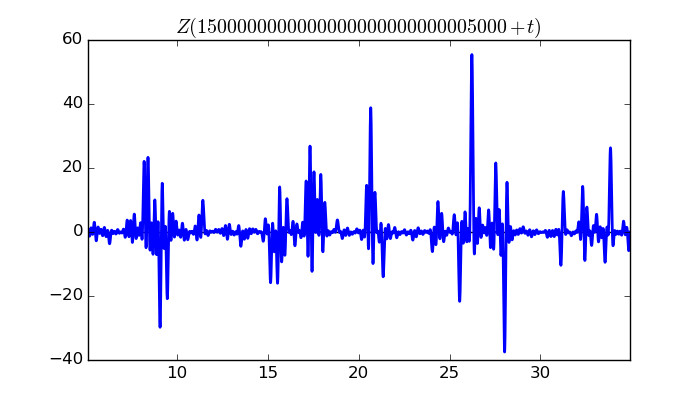
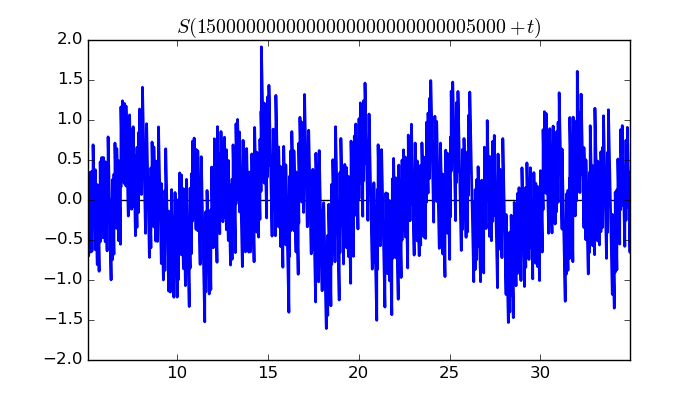
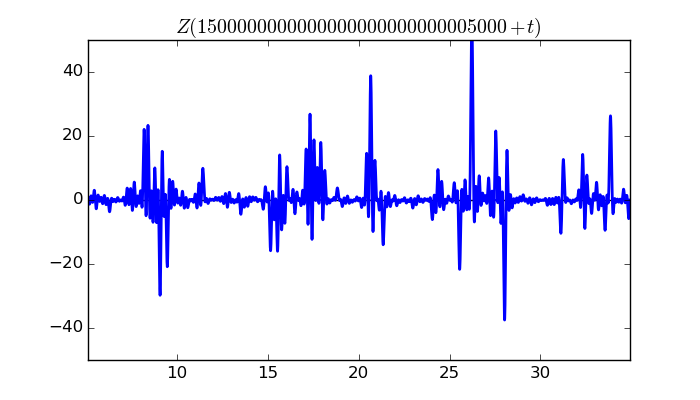
$\zeta(1/2 + it)$ around $t = 1500000000000000000000000005000 \approx 1.5 \times 10^{ 30 }$
Largest value of $Z(t)$ in this graph:-56.48299812
Value of $t$ for which the maximum occurs:1500000000000000000000000005035.98626172
Value of $\zeta(1/2 + it)$:$56.43803979 + 2.25316255i$
Maximum of $S(t)$ in this range:1.914417045
$\zeta(1/2 + it)$ around $t = 16000000000000000000000000280 \approx 1.6 \times 10^{ 28 }$
Largest value of $Z(t)$ in this graph:-52.9603908
Value of $t$ for which the maximum occurs:16000000000000000000000000285.464371094
Value of $\zeta(1/2 + it)$:$51.60156147 + 11.91980901i$
Maximum of $S(t)$ in this range:1.911026801
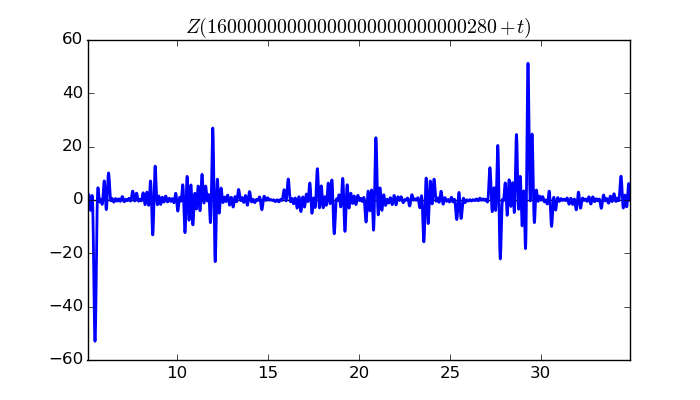
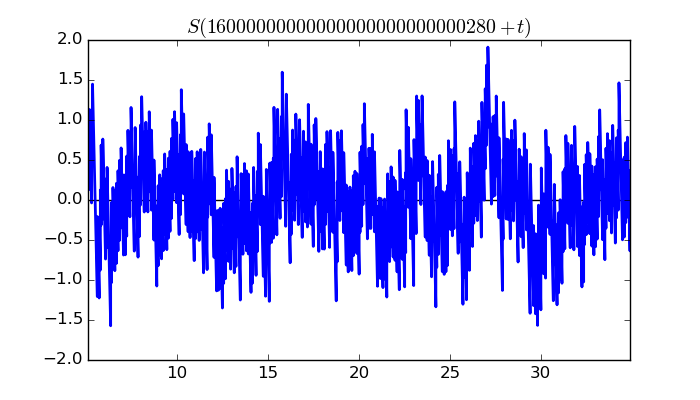
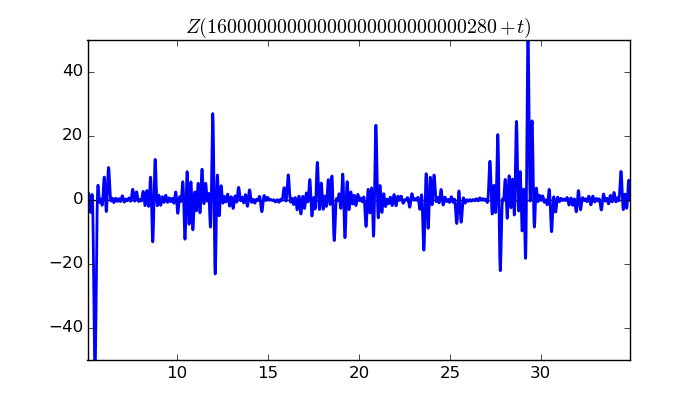
$\zeta(1/2 + it)$ around $t = 10000000000000000000000000080 \approx 1.0 \times 10^{ 28 }$
Largest value of $Z(t)$ in this graph:64.47512928
Value of $t$ for which the maximum occurs:10000000000000000000000000085.331996094
Value of $\zeta(1/2 + it)$:$60.34910751 - 22.69421773i$
Maximum of $S(t)$ in this range:1.910704816
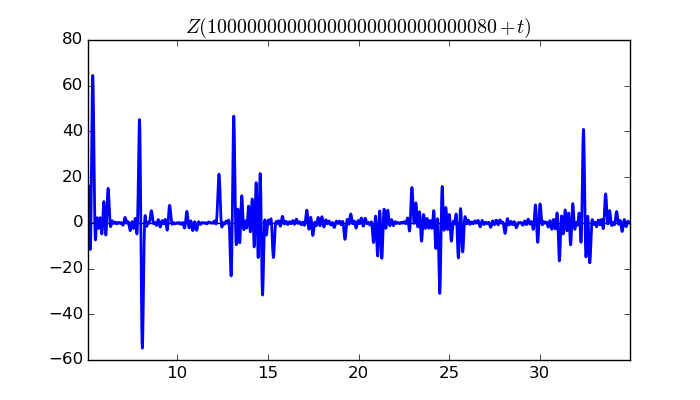
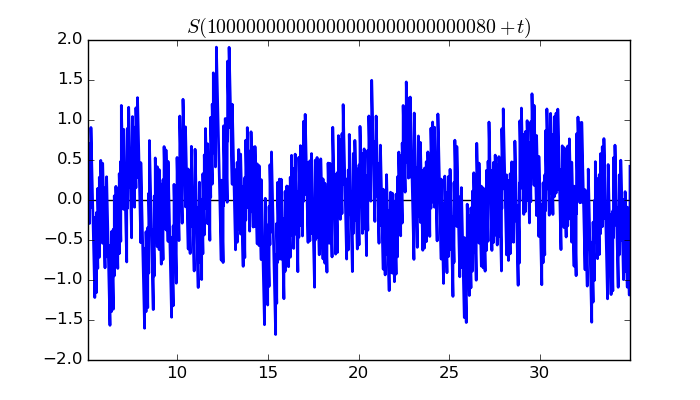
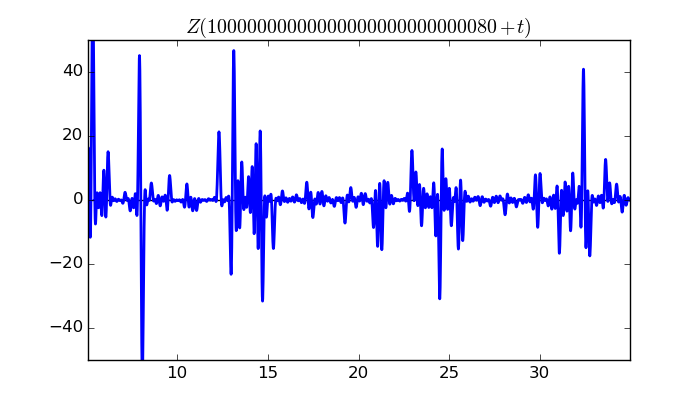
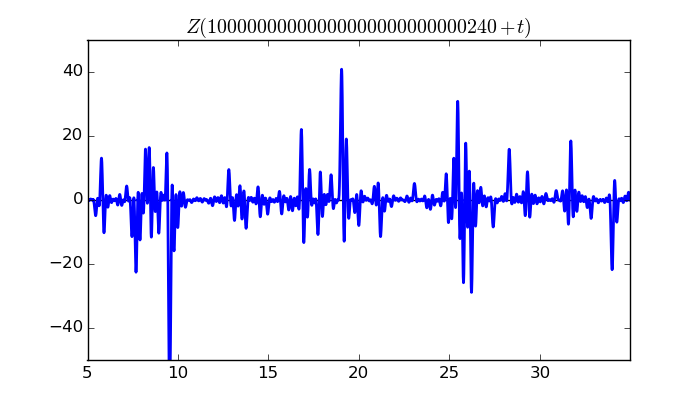
$\zeta(1/2 + it)$ around $t = 10000000000000000000000000240 \approx 1.0 \times 10^{ 28 }$
Largest value of $Z(t)$ in this graph:-61.44358057
Value of $t$ for which the maximum occurs:10000000000000000000000000249.555996094
Value of $\zeta(1/2 + it)$:$50.11324921 - 35.55243797i$
Maximum of $S(t)$ in this range:1.903679777
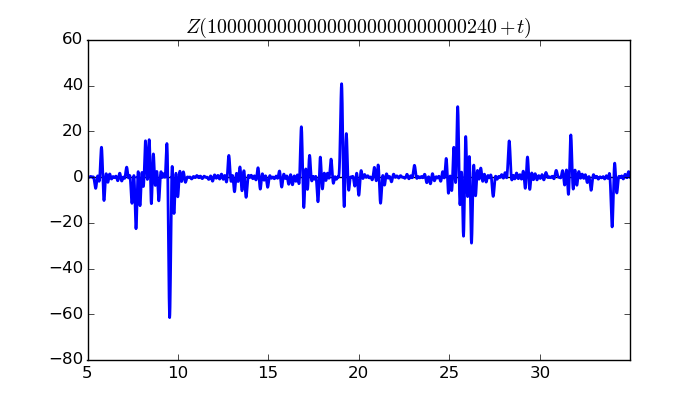
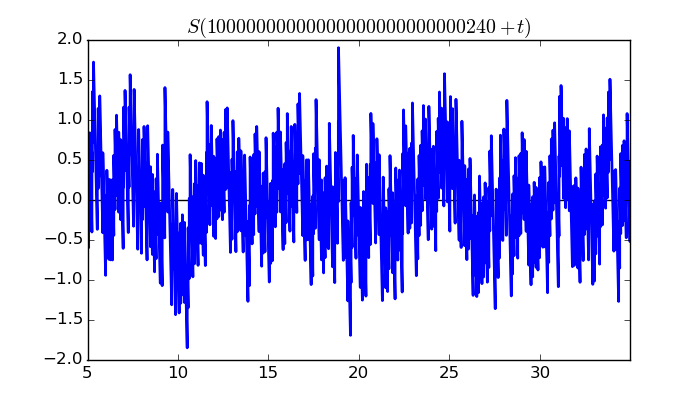
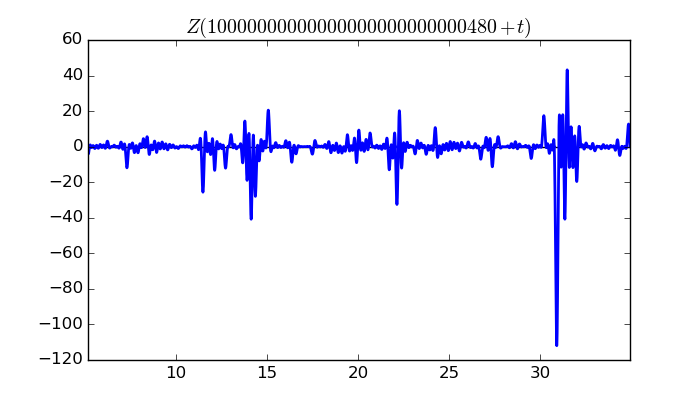
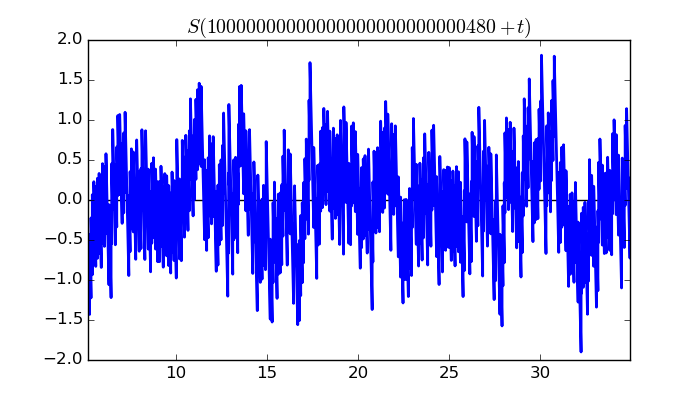
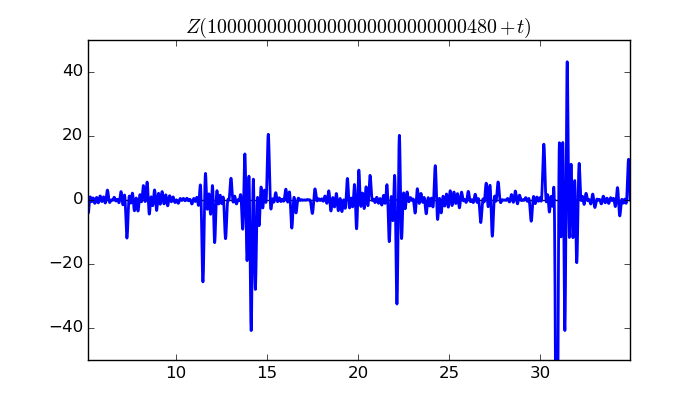
$\zeta(1/2 + it)$ around $t = 10000000000000000000000000480 \approx 1.0 \times 10^{ 28 }$
Largest value of $Z(t)$ in this graph:-111.9397727
Value of $t$ for which the maximum occurs:10000000000000000000000000510.91416016
Value of $\zeta(1/2 + it)$:$24.10761727 + 109.3130161i$
Maximum of $S(t)$ in this range:-1.899419353
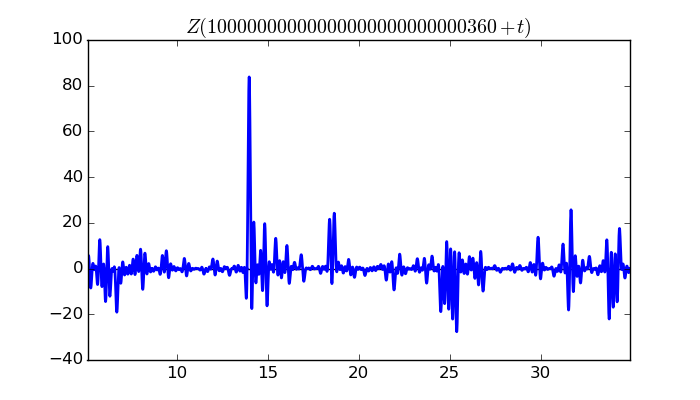
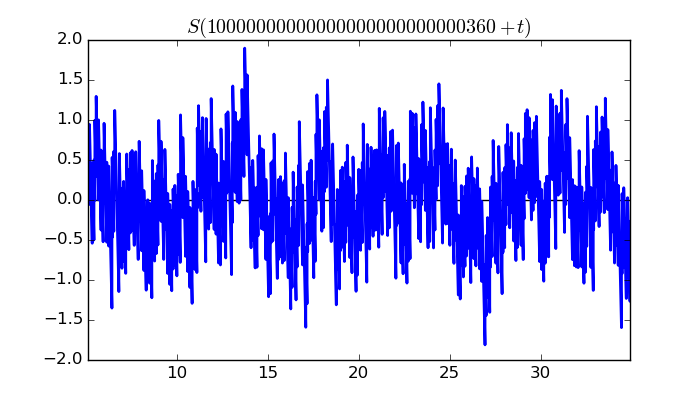
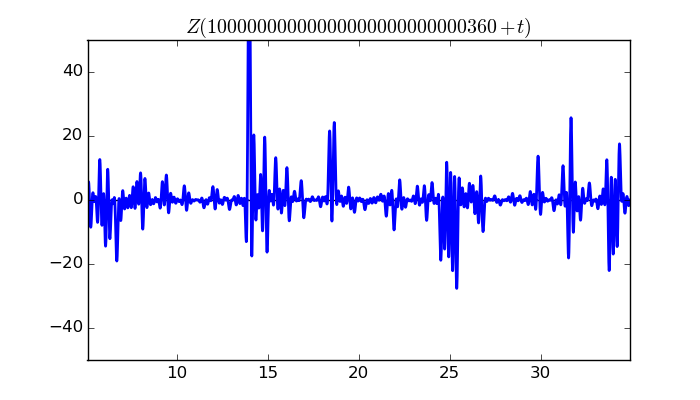
$\zeta(1/2 + it)$ around $t = 10000000000000000000000000360 \approx 1.0 \times 10^{ 28 }$
Largest value of $Z(t)$ in this graph:83.8344958
Value of $t$ for which the maximum occurs:10000000000000000000000000373.98409766
Value of $\zeta(1/2 + it)$:$18.1033582 + 81.85652758i$
Maximum of $S(t)$ in this range:1.898016433
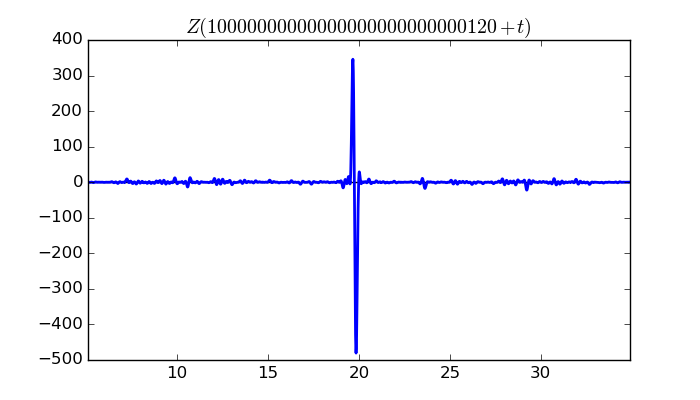
$\zeta(1/2 + it)$ around $t = 10000000000000000000000000120 \approx 1.0 \times 10^{ 28 }$
Largest value of $Z(t)$ in this graph:-480.5116167
Value of $t$ for which the maximum occurs:10000000000000000000000000139.82914453
Value of $\zeta(1/2 + it)$:$184.8801747 - 443.5208392i$
Maximum of $S(t)$ in this range:-1.890637995
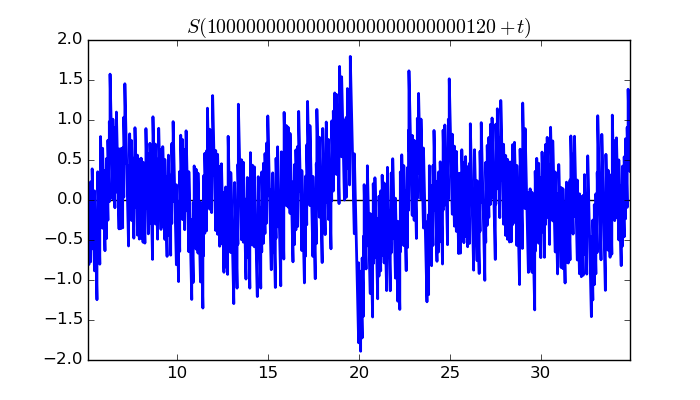
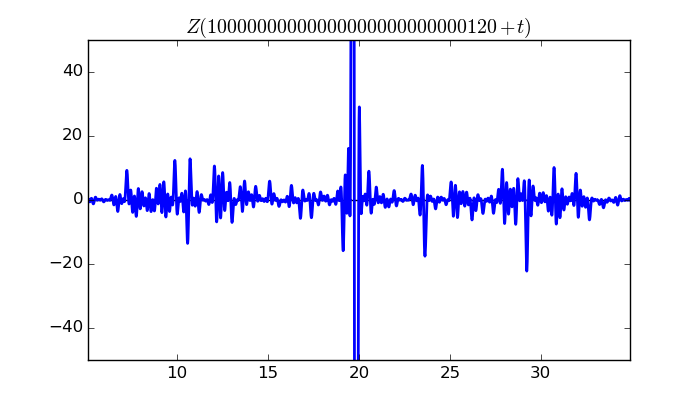
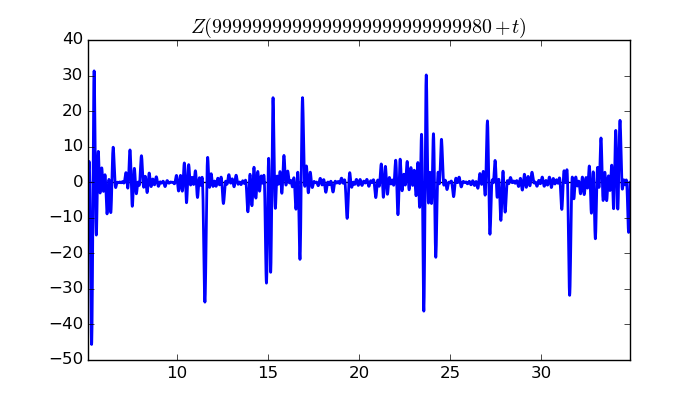
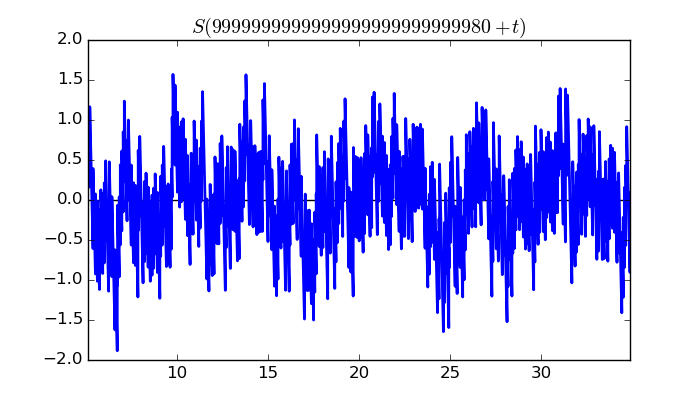
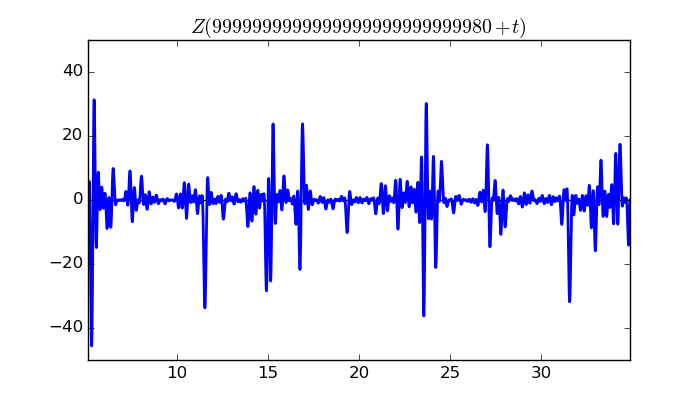
$\zeta(1/2 + it)$ around $t = 9999999999999999999999999980 \approx 1.0 \times 10^{ 28 }$
Largest value of $Z(t)$ in this graph:-45.62660934
Value of $t$ for which the maximum occurs:9999999999999999999999999985.290347656
Value of $\zeta(1/2 + it)$:$39.99671851 + 21.95563683i$
Maximum of $S(t)$ in this range:-1.884375111
