LSWsim

Simulate arbitrary locally stationary wavelet process.

DESCRIPTION

USAGE

LSWsim(spec)

REQUIRED ARGUMENTS

spec

An object of class wd (the NDWT kind) which contains the spectral information for simulating your process. See examples below on how to create and manipulate this object.

OPTIONAL ARGUMENTS

VALUE

DETAILS

The input object, spec, is a wd class object which contains a spectral description. In particular, all coefficients must be nonnegative and LSWsim() checks for this and returns an error if it is not so. Other than that the spectrum can contain pretty much anything. An object of this type can be easily created by the convenience routine cns. This creates an object of the correct structure but all elements are initially set to zero. The spectrum structure spec can then be filled by using the putD function.

The function works by first checking for non-negativity. Then it takes the square root of all coefficients. Then it multiplies all coefficients by a standard normal variate (from rnorm()) and multiples the finest level by 2, the next finest by 4, the next by 8 and so on. (This last scalar multiplication is intended to undo the effect of the average basis averaging which combines cofficients but divides by two at each combination). Finally, the modified spectral object is subjected to the convert function which converts the object from a wd time-ordered NWDT object to a wst packet-ordered object which can then be inverted using AvBasis.

Note that the NDWT transforms in WaveThresh are periodic so that the process that one simulates with this function is also periodic.

RELEASE

SEE ALSO

EXAMPLES

#
# Suppose we want to create a LSW process of length 1024 and with a spectral
# structure that has a squared sinusoidal character at level 4 and a burst of
# activity from time 800 for 100 observations at scale 9 (remember for a
# process of length 1024 there will be 9 resolution levels (since 2^10=1024)
# where level 9 is the finest and level 0 is the coarsest).
#
# First we will create an empty spectral structure for series of 1024 observations
#
#
myspec <- cns(1024)
#
# If you plot it you'll get a null spectrum (since every spectral entry is zero)
#
plot(myspec, main="My Spectrum")
#
#
# Now let's add the desired spectral structure
#
# First the squared sine (remember spectra are positive)
#
myspec <- putD(myspec, level=4, sin(seq(from=0, to=4*pi, length=1024))^2)
#
# Let's create a burst of spectral info of size 1 from 800 to 900. Remember
# the whole vector has to be of length 1024.
#
burstat800 <- c(rep(0,800), rep(1,100), rep(0,124))
#
# Insert this (00000111000) type vector into the spectrum at fine level 9
#
myspec <- putD(myspec, level=9, v=burstat800)
#
# Now it's worth plotting this spectrum
#
plot(myspec, main="My Spectrum")

#
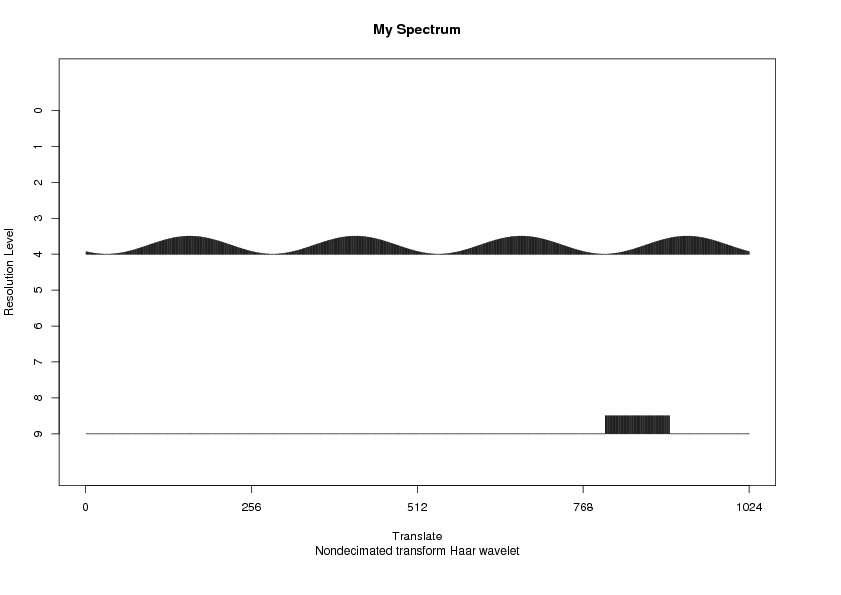# The squared sinusoid at level 4 and the burst at level 9 can clearly
# be seen
#
#
# Now simulate a random process with this spectral structure.
#
myLSWproc <- LSWsim(myspec)
#
# Let's see what it looks like
#
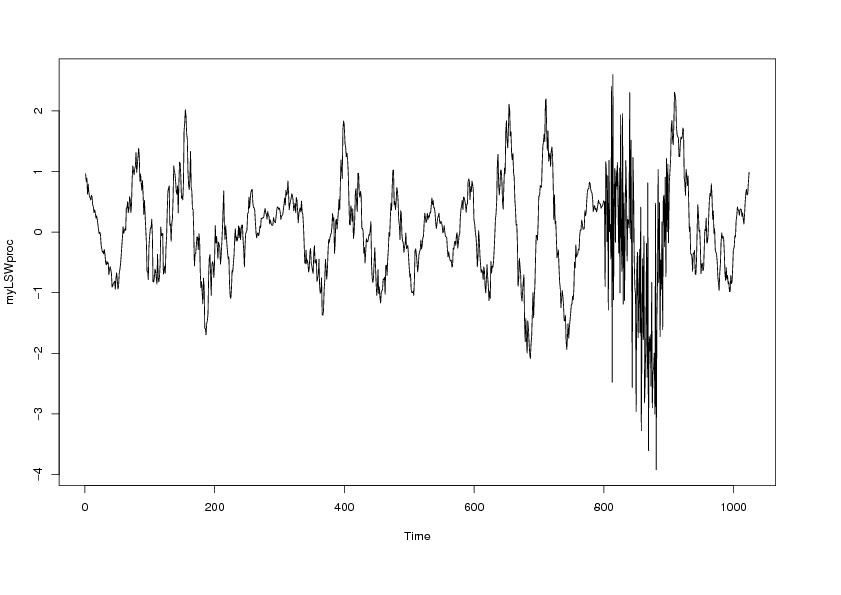
ts.plot(myLSWproc)

#
#
# The burst is very clear but the sinusoidal structure is less apparent.
# That's basically it.
#
# You could now play with the spectrum (ie alter it) or simulate another process
# from it.
#
# [The following is somewhat of an aside but useful to those more interested
# in the LSW scene. We could now ask, so what? So you can simulate an
# LSW process. How can I be sure that it is doing so correctly? Well, here is
# a partial, computational, answer. If you simulate many realisations from the
# same spectral structure, estimate its spectrum, and then average those
# estimates then the average should tend to the spectrum you supplied. Here is a
# little function to do this (just for Haar but this function could easily be
# developed to be more general):
#
checkmyews <- function(spec, nsim=10){
        ans <- cns(2^nlevels(spec))
        for(i in 1:nsim)        {
                cat(".")
                LSWproc <- LSWsim(spec)
                ews <- ewspec(LSWproc, filter.number=1, family="DaubExPhase",
                        WPsmooth=F)
                ans$D <- ans$D + ews$S$D
                ans$C <- ans$C + ews$S$C
        }
        ans$D <- ans$D/nsim
        ans$C <- ans$C/nsim
        ans
}
# If you supply it with a spectral structure (like myspec)
# from above and do enough simulations you'll get something looking like
# the original myspec structure. E.g. try
#
plot(checkmyews(myspec, nsim=100))
#
# for fun. This type of check also gives you some idea of how much data
# you really need for LSW estimation for given spectral structures.]
#