WaveThresh
Help
MaNoVe.wst
Make Node Vector (using Coifman-Wickerhauser best-basis type algorithm) on
packet ordered non-decimated wavelet transform object
DESCRIPTION
This method function chooses a ``best-basis'' using the
Coifman-Wickerhauser (1992) algorithm applied
to wavelet packet wst objects.
USAGE
MaNoVe.wst(wst, entropy = Shannon.entropy, verbose = F, stopper = F,
alg = "C")
REQUIRED ARGUMENTS
-
wst
- the wst object for which you wish to find the
best-basis for.
OPTIONAL ARGUMENTS
- entropy
- A function for computing the entropy of a vector (usually
the function Shannon.entropy is used but it
doesn't need to be).
- verbose
- whether or not to print out informative error messages.
- stopper
- whether the computations are stopped after each packet. This can be
useful in conjunction with the
verbose argument
so as to see computations one packet at a time.
- alg
- If
"C" then fast compiled C code is used (in which case
the entropy function is ignored and the C code
uses an (internal) Shannon entropy). Otherwise slower S code is used
but an arbitrary entropy argument can be used.
VALUE
A node vector
object. This specifies which packets have been selected.
RELEASE
Version 3.6 Copyright Guy Nason
SEE ALSO
MaNoVe,
wst object,
wst.
EXAMPLES
#
# What follows is a simulated denoising example. We first create our
# "true" underlying signal, v. Then we add some noise to it with a signal
# to noise ratio of 6. Then we take the packet-ordered non-decimated wavelet
# transform and then threshold that.
#
# Then, to illustrate this function, we computes is "best-basis" node vector
# and use that to invert the packet-ordered NDWT using this basis. As a
# comparison we also use the Average Basis method
# (of Coifman and Donoho, 1995).
#
# NOTE: It is IMPORTANT to note that this example DOES not necessarily
# use an appropriate or good threshold or necessarily the right underlying
# wavelet. I am trying to show the general idea and please do not "quote" this
# example in literature saying that this is the way that WaveThresh (or
# any of the associated authors whose methods it attempts to implement)
# does it. Proper denoising requires a lot of care and thought.
#
#
# Here we go....
#
# Create an example vector (the Donoho and Johnstone heavisine function)
#
v <- DJ.EX()$heavi
#
# Add some noise with a SNR of 6
#
vnoise <- v + rnorm(length(v), 0, sd=sqrt(var(v))/6)
#
# Take packet-ordered non-decimated wavelet transform (note default wavelet
# used which might not be the best option for denoising performance).
#
vnwst <- wst(vnoise)
#
# Let's take a look at the wavelet coefficients of vnoise
#
plot(vnwst)
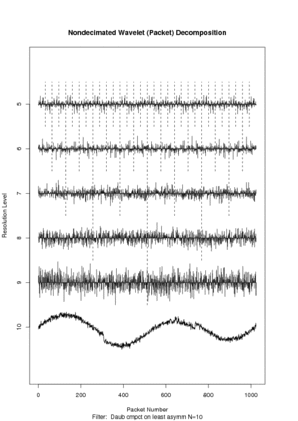 #
# Wow! A huge number of coefficients, but mostly all noise.
#
#
# Threshold the resultant NDWT object.
# (Once again default arguments are used which are certainly not optimal).
#
vnwstT <- threshold(vnwst)
#
# Let's have a look at the thresholded wavelet coefficients
#
plot(vnwstT)
#
# Wow! A huge number of coefficients, but mostly all noise.
#
#
# Threshold the resultant NDWT object.
# (Once again default arguments are used which are certainly not optimal).
#
vnwstT <- threshold(vnwst)
#
# Let's have a look at the thresholded wavelet coefficients
#
plot(vnwstT)
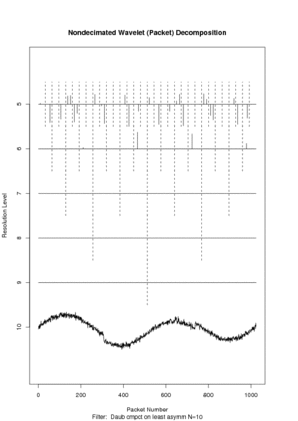 #
# Ok, a lot of the coefficients have been removed as one would expect with
# universal thresholding
#
#
# Now select packets for a basis using a Coifman-Wickerhauser algorithm
#
vnnv <- MaNoVe(vnwstT)
#
# Let's have a look at which packets got selected
#
vnnv
# Level : 9 Action is R (getpacket Index: 1 )
# Level : 8 Action is L (getpacket Index: 2 )
# Level : 7 Action is L (getpacket Index: 4 )
# Level : 6 Action is L (getpacket Index: 8 )
# Level : 5 Action is R (getpacket Index: 17 )
# Level : 4 Action is L (getpacket Index: 34 )
# Level : 3 Action is L (getpacket Index: 68 )
# Level : 2 Action is R (getpacket Index: 137 )
# Level : 1 Action is R (getpacket Index: 275 )
# There are 10 reconstruction steps
#
# So, its not the regular decimated wavelet transform!
#
# Let's invert the representation with respect to this basis defined by
# vnnv
#
vnwrIB <- InvBasis(vnwstT, vnnv)
#
# And also, for completeness let's do an Average Basis reconstruction.
#
vnwrAB <- AvBasis(vnwstT)
#
# Let's look at the Integrated Squared Error in each case.
#
sum( (v - vnwrIB)^2)
# [1] 386.2501
#
sum( (v - vnwrAB)^2)
# [1] 328.4520
#
# So, for this limited example the average basis method does better. Of course,
# for *your* simulation it could be the other way round. "Occasionally", the
# inverse basis method does better. When does this happen? A good question.
#
# Let's plot the reconstructions and also the original
#
plot(vnwrIB, type="l")
lines(vnwrAB, lty=2)
lines(v, lty=3)
#
# Ok, a lot of the coefficients have been removed as one would expect with
# universal thresholding
#
#
# Now select packets for a basis using a Coifman-Wickerhauser algorithm
#
vnnv <- MaNoVe(vnwstT)
#
# Let's have a look at which packets got selected
#
vnnv
# Level : 9 Action is R (getpacket Index: 1 )
# Level : 8 Action is L (getpacket Index: 2 )
# Level : 7 Action is L (getpacket Index: 4 )
# Level : 6 Action is L (getpacket Index: 8 )
# Level : 5 Action is R (getpacket Index: 17 )
# Level : 4 Action is L (getpacket Index: 34 )
# Level : 3 Action is L (getpacket Index: 68 )
# Level : 2 Action is R (getpacket Index: 137 )
# Level : 1 Action is R (getpacket Index: 275 )
# There are 10 reconstruction steps
#
# So, its not the regular decimated wavelet transform!
#
# Let's invert the representation with respect to this basis defined by
# vnnv
#
vnwrIB <- InvBasis(vnwstT, vnnv)
#
# And also, for completeness let's do an Average Basis reconstruction.
#
vnwrAB <- AvBasis(vnwstT)
#
# Let's look at the Integrated Squared Error in each case.
#
sum( (v - vnwrIB)^2)
# [1] 386.2501
#
sum( (v - vnwrAB)^2)
# [1] 328.4520
#
# So, for this limited example the average basis method does better. Of course,
# for *your* simulation it could be the other way round. "Occasionally", the
# inverse basis method does better. When does this happen? A good question.
#
# Let's plot the reconstructions and also the original
#
plot(vnwrIB, type="l")
lines(vnwrAB, lty=2)
lines(v, lty=3)
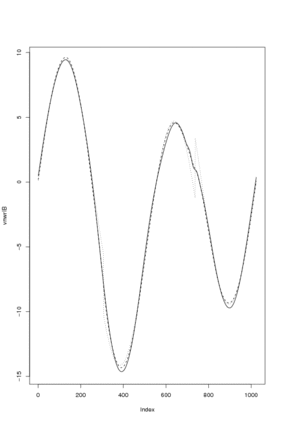 #
# The dotted line is the original. Neither reconstruction picks up the
# spikes in heavisine very well. The average basis method does track the
# original signal more closely though.
#
#
# The dotted line is the original. Neither reconstruction picks up the
# spikes in heavisine very well. The average basis method does track the
# original signal more closely though.
#
 #
# Wow! A huge number of coefficients, but mostly all noise.
#
#
# Threshold the resultant NDWT object.
# (Once again default arguments are used which are certainly not optimal).
#
vnwstT <- threshold(vnwst)
#
# Let's have a look at the thresholded wavelet coefficients
#
plot(vnwstT)
#
# Wow! A huge number of coefficients, but mostly all noise.
#
#
# Threshold the resultant NDWT object.
# (Once again default arguments are used which are certainly not optimal).
#
vnwstT <- threshold(vnwst)
#
# Let's have a look at the thresholded wavelet coefficients
#
plot(vnwstT)
 #
# Ok, a lot of the coefficients have been removed as one would expect with
# universal thresholding
#
#
# Now select packets for a basis using a Coifman-Wickerhauser algorithm
#
vnnv <- MaNoVe(vnwstT)
#
# Let's have a look at which packets got selected
#
vnnv
# Level : 9 Action is R (getpacket Index: 1 )
# Level : 8 Action is L (getpacket Index: 2 )
# Level : 7 Action is L (getpacket Index: 4 )
# Level : 6 Action is L (getpacket Index: 8 )
# Level : 5 Action is R (getpacket Index: 17 )
# Level : 4 Action is L (getpacket Index: 34 )
# Level : 3 Action is L (getpacket Index: 68 )
# Level : 2 Action is R (getpacket Index: 137 )
# Level : 1 Action is R (getpacket Index: 275 )
# There are 10 reconstruction steps
#
# So, its not the regular decimated wavelet transform!
#
# Let's invert the representation with respect to this basis defined by
# vnnv
#
vnwrIB <- InvBasis(vnwstT, vnnv)
#
# And also, for completeness let's do an Average Basis reconstruction.
#
vnwrAB <- AvBasis(vnwstT)
#
# Let's look at the Integrated Squared Error in each case.
#
sum( (v - vnwrIB)^2)
# [1] 386.2501
#
sum( (v - vnwrAB)^2)
# [1] 328.4520
#
# So, for this limited example the average basis method does better. Of course,
# for *your* simulation it could be the other way round. "Occasionally", the
# inverse basis method does better. When does this happen? A good question.
#
# Let's plot the reconstructions and also the original
#
plot(vnwrIB, type="l")
lines(vnwrAB, lty=2)
lines(v, lty=3)
#
# Ok, a lot of the coefficients have been removed as one would expect with
# universal thresholding
#
#
# Now select packets for a basis using a Coifman-Wickerhauser algorithm
#
vnnv <- MaNoVe(vnwstT)
#
# Let's have a look at which packets got selected
#
vnnv
# Level : 9 Action is R (getpacket Index: 1 )
# Level : 8 Action is L (getpacket Index: 2 )
# Level : 7 Action is L (getpacket Index: 4 )
# Level : 6 Action is L (getpacket Index: 8 )
# Level : 5 Action is R (getpacket Index: 17 )
# Level : 4 Action is L (getpacket Index: 34 )
# Level : 3 Action is L (getpacket Index: 68 )
# Level : 2 Action is R (getpacket Index: 137 )
# Level : 1 Action is R (getpacket Index: 275 )
# There are 10 reconstruction steps
#
# So, its not the regular decimated wavelet transform!
#
# Let's invert the representation with respect to this basis defined by
# vnnv
#
vnwrIB <- InvBasis(vnwstT, vnnv)
#
# And also, for completeness let's do an Average Basis reconstruction.
#
vnwrAB <- AvBasis(vnwstT)
#
# Let's look at the Integrated Squared Error in each case.
#
sum( (v - vnwrIB)^2)
# [1] 386.2501
#
sum( (v - vnwrAB)^2)
# [1] 328.4520
#
# So, for this limited example the average basis method does better. Of course,
# for *your* simulation it could be the other way round. "Occasionally", the
# inverse basis method does better. When does this happen? A good question.
#
# Let's plot the reconstructions and also the original
#
plot(vnwrIB, type="l")
lines(vnwrAB, lty=2)
lines(v, lty=3)
 #
# The dotted line is the original. Neither reconstruction picks up the
# spikes in heavisine very well. The average basis method does track the
# original signal more closely though.
#
#
# The dotted line is the original. Neither reconstruction picks up the
# spikes in heavisine very well. The average basis method does track the
# original signal more closely though.
#