LocalSpec.wd

Compute Nason and Silverman raw or smoothed wavelet periodogram.

DESCRIPTION

This function computes the Nason and Silverman raw or smoothed wavelet periodogram as described by Nason and Silverman (1995).

USAGE

LocalSpec.wd(wdS, lsmooth="none", nlsmooth=F, prefilter=T,
  verbose=F, lw.number=wdS$filter$filter.number,
  lw.family=wdS$filter$family, nlw.number=wdS$filter$filter.number,
  nlw.family=wdS$filter$family, nlw.policy="universal",
  nlw.levels=3:(nlevels(wdS) - 1), nlw.type="hard", nlw.by.level=F,
  nlw.value=0, nlw.dev=var, nlw.boundary=F, nlw.verbose=F,
  nlw.cvtol=0.01, nlw.Q=0.05, nlw.alpha=0.05, nlw.transform=I,
  nlw.inverse=I, debug.spectrum=F)

REQUIRED ARGUMENTS

wdS

The stationary wavelet transform object that you want to smooth or square.

OPTIONAL ARGUMENTS

lsmooth

Controls the LINEAR smoothing. There are three options: "none", "Fourier" and "wavelet". They are described below. Note that Fourier begins with a capital "F".

nlsmooth

A switch to turn on (or off) the NONLINEAR wavelet shrinkage of (possibly LINEAR smoothed) local power coefficients. This option is either T (to turn on the smoothing) or F (to turn it off).

prefilter

If T then apply a prefilter to the actual stationary wavelet coefficients at each level. This is a low-pass filter that cuts off all frequencies above the highest frequency allowed by the (Littlewood-Paley) wavelet that bandpassed the current level coefficients. If F then no prefilter is applied.

verbose

If T then the function chats about what it is doing. Otherwise it is silent.

lw.number

If wavelet LINEAR smoothing is used then this option controls the filter number of the wavelet within the family used to perform the LINEAR wavelet smoothing.

lw.family

If wavelet LINEAR smoothing is used then this option controls the family of the wavelet used to perform the LINEAR wavelet smoothing.

nlw.number

If NONLINEAR wavelet smoothing is also used then this option controls the filter number of the wavelet used to perform the wavelet shrinkage.

nlw.family

If NONLINEAR wavelet smoothing is also used then this option controls the family of the wavelet used to perform the wavelet shrinkage.

nlw.policy

If NONLINEAR wavelet smoothing is also used then this option controls the levels to use when performing wavelet shrinkage (see threshold.wd for different policy choices).

nlw.levels

If NONLINEAR wavelet smoothing is also used then this option controls the levels to use when performing wavelet shrinkage (see threshold.wd for a detailed description of how levels can be chosen).

nlw.type

If NONLINEAR wavelet smoothing is also used then this option controls the type of thresholding used in the wavelet shrinkage (either "hard" or "soft", but see threshold.wd for a list).

nlw.by.level

If NONLINEAR wavelet smoothing is also used then this option controls whether level-by-level thresholding is used or if one threshold is chosen for all levels (see threshold.wd).

nlw.value

If NONLINEAR wavelet smoothing is also used then this option controls if a manual (or similar) policy is supplied to nlw.policy then the nlw.value option carries the manual threshold value (see threshold.wd).

nlw.dev

If NONLINEAR wavelet smoothing is also used then this option controls the type of variance estimator that is used in wavelet shrinkages (see threshold.wd). One possibility is the Splus var() function, another is the WaveThresh function madmad().

nlw.boundary

If NONLINEAR wavelet smoothing is also used then this option controls whether boundary coefficients are also thresholded (see threshold.wd).

nlw.verbose

If NONLINEAR wavelet smoothing is also used then this option controls whether the threshold function prints out messages as it thresholds levels (see threshold.wd).

nlw.cvtol

If NONLINEAR wavelet smoothing is also used then this option controls the optimization tolerance is cross-validation wavelet shrinkage is used (see threshold.wd).

nlw.Q

If NONLINEAR wavelet smoothing is also used then this option controls the Q value for wavelet shrinkage (see threshold.wd).

nlw.alpha

If NONLINEAR wavelet smoothing is also used then this option controls the alpha value for wavelet shrinkage (see threshold.wd).

nlw.transform

If NONLINEAR wavelet smoothing is also used then this option controls a transformation that is applied to the squared (and possibly linear smoothed) stationary wavelet coefficients before shrinkage. So, for example, you might want to set nlw.transform=log to perform wavelet shrinkage on the logs of the squared (and possibly linear smoothed) stationary wavelet coefficients.

nlw.inverse

If NONLINEAR wavelet smoothing is also used then this option controls the inverse transformation that is applied to the wavelet shrunk coefficients before they are put back into the stationary wavelet transform structure. So, for example, if the nlw.transform is log() you should set the inverse to nlw.inverse=exp.

debug.spectrum

If this option is T then spectrum plots are produced at each stage of the squaring/smoothing. Therefore if you put in the non-decimated wavelet transform of white noise you can get a fair idea of how the coefficients are filtered at each stage.

VALUE

SIDE EFFECTS

DETAILS

This function attempts to produce a picture of local time-scale power of a signal. There are two main components to this function: linear smoothing of squared coefficients and non-linear smoothing of these. Neither, either or both of these components may be used to process the data. The function expects a non-decimated wavelet transform object (of class wd, type="station") such as that produced by the wd() function with the type option set to "station". The following paragraphs describe the various methods of smoothing.

LINEAR SMOOTHING. There are three varieties of linear smoothing. None simply squares the coefficients. Fourier and wavelet apply linear smoothing methods in accordance to the prescription given in Nason and Silverman (1995). Each level in the SWT corresponds to a band-pass filtering to a frequency range [sl, sh]. After squaring we obtain power in the range [0, 2sl] and [2sl, 2sh]. The linear smoothing gets rid of the power in [2sl, 2sh]. The Fourier method simply applies a discrete Fourier transform (rfft) and cuts off frequencies above 2sl. The wavelet method is a bit more suble. The DISCRETE wavelet transform is taken of a level (i) and all levels within the DWT, j, where j>i are set to zero and then the inverse is taken. Approximately this performs the same operation as the Fourier method only faster. By default the same wavelets are used to perform the linear smoothing as were used to compute the stationary wavelet transform in the first place. This can be changed by altering lw.number and lw.family.

NONLINEAR SMOOTHING. After either of the linear smoothing options above it is possible to use wavelet shrinkage upon each level in the squared (and possibly Fourier or wavelet linear smoothed) to denoise the coefficients. This process is akin to smoothing the ordinary periodogram. All the usual wavelet shrinkage options are available as nlw.* where * is one of the usual threshold.wd options. By default the same wavelets are used to perform the wavelet shrinkage as were used to compute the non-decimated wavelet transform. These wavelets can be replaced by altering nlw.number and nlw.family. Also, it is possible to transform the squared (and possibly smoothed coefficients) before applying wavelet shrinkage. The transformation is effected by supplying an appropriate transformation function (AND ITS INVERSE) to nlw.transform and nlw.inverse. (For example, nlw.transform=log and nlw.inverse=exp might be a good idea).

RELEASE

REFERENCES

Nason and Silverman, (1995).

SEE ALSO

EXAMPLES

#
# This function is obsolete. See ewspec()
#
# Compute the raw periodogram of the BabyECG
# data using the Daubechies least-asymmetric wavelet $N=10$.
#
> babywdS <- wd(BabyECG, filter.number=10, family="DaubLeAsymm", type="station")
> babyWP <- LocalSpec(babywdS, lsmooth = "none", nlsmooth = F)
> plot(babyWP, main="Raw Wavelet Periodogram of Baby ECG") 

#
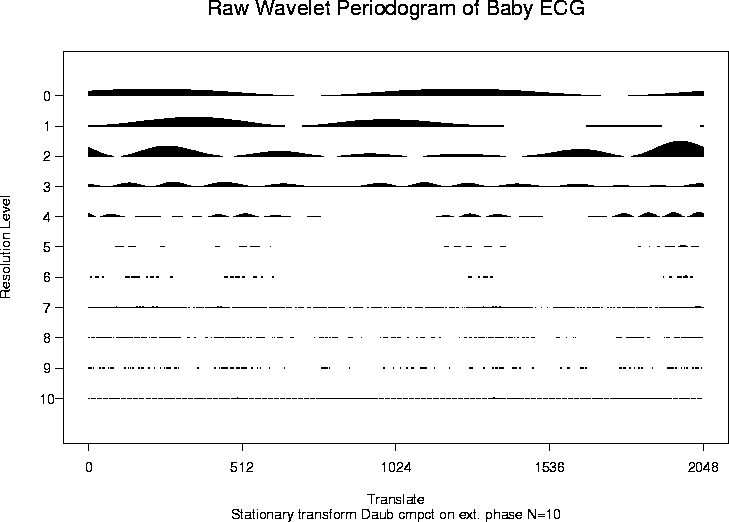# Note that the lower levels of this plot are too large. This is partly because
# there are "too many" coefficients at the lower levels. For a better
# picture of the local spectral properties of this time series see
# the examples section of ewspec
#
# Other results of this function can be seen in the paper by
# Nason and Silverman (1995) above.
#